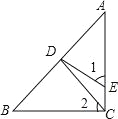
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,DE⊥AB于点D,交AC于点E.
(1)若BC=3,AC=4,求CD的长;
(2)求证:∠1=∠2.
参考答案:
【答案】(1)2.5(2)∠1=∠2
【解析】
试题分析:(1)由勾股定理求出AB,再根据直角三角形斜边上的中线等于斜边的一半解答即可;
(2)由直角三角形的锐角关系和等腰三角形的性质即可得出结论.
试题解析:(1)解:∵∠ACB=90°,BC=3,AC=4,
∴AB=![]() =5,
=5,
∵CD是AB边上的中线,
∴CD=![]() AB=2.5;
AB=2.5;
(2)证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵DE⊥AB,
∴∠A+∠1=90°,
∴∠B=∠1,
∵CD是AB边上的中线,
∴BD=CD,
∴∠B=∠2,
∴∠1=∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+ax﹣1=0的根的情况是( )
A.没有实数根
B.只有一个实数根
C.有两个相等的实数根
D.有两个不相等的实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=
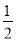 x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(27,9)阴影三角形部分的面积从左向右依次为S1、S2、S3…Sn,则第4个正方形的边长是______,Sn的值为______.
x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(27,9)阴影三角形部分的面积从左向右依次为S1、S2、S3…Sn,则第4个正方形的边长是______,Sn的值为______.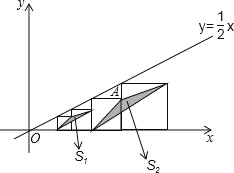
-
科目: 来源: 题型:
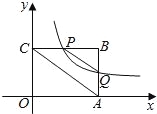
查看答案和解析>>【题目】如图,平面直角坐标系中,矩形OABC的一边OA在x轴上,点B的坐标为(4,3),双曲线
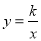 (x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q
(x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q(1)若P为边BC的中点,求双曲线的函数表达式及点Q的坐标;
(2)求k的取值范围;
(3)连接PQ,AC,判断:PQ∥AC是否总成立?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中不正确的是( ).
A.-3.14既是负数,分数,也是有理数
B.0既不是正数,也不是负数,但是整数
C.-2000既是负数,也是整数,但不是有理数
D.0是非正数 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,C为直线l上的一点,A、B为直线l外的两点,过A、B两点分别作直线l的垂线,垂足分别为点D、E,连接BC、AB,AB交直线l于点F,AC=BC,AD=CE.
求证:(1)CE=BE+DE;
(2)AC⊥BC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列说法:①0是整数;②-3.5是负分数;③5.4不是正数;④自然数一定是正数;⑤负分数一定是负有理数,其中正确的有( ).
A.1个
B.2个
C.3个
D.4个
相关试题

