【题目】如图,在五边形ABCDE中,已知∠BAE=120°,∠B=∠E=90°,AB=BC=2,AE=DE=4,在BC、DE上分别找一点M、N,若要使△AMN的周长最小时,则△AMN的最小周长为______.

参考答案:
【答案】4![]()
【解析】分析:利用点的对称,让△AMN的三边在同一直线上,即作出A关于BC和ED的对称点A′,A″,即可得出最短路线,再利用勾股定理,求出即可.
详解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交ED于N,则A′A″即为△AMN的周长最小值.
过A′作EA延长线的垂线,垂足为H,

∵AB=BC=2,AE=DE=4,
∴AA′=2BA=4,AA″=2AE=8,
则Rt△A′HA中,
∵∠EAB=120°,
∴∠HAA′=60°,
∵A′H⊥HA,
∴∠AA′H=30°,
∴AH=![]() AA′=2,
AA′=2,
∴A′H=![]() ,,
,,
A″H=2+8=10,
∴A′A″=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 称为第 1 个三角形,它的周长是 1,以它的三边中点为顶点组成第 2 个三角形,再以第 2 个三角形的三边中点为顶点组成第 3 个三角形,以此类推,则第 2019 个三角形的周长为( )
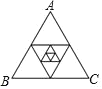
A.
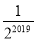 B.
B.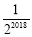 C.
C. D.
D.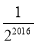
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量
 (单位:个)与销售单价
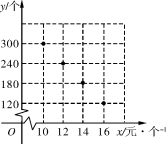
(单位:个)与销售单价 (单位:元/个)之间的对应关系如图所示:
(单位:元/个)之间的对应关系如图所示:(1)
 与
与 之间的函数关系是 .
之间的函数关系是 .(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润
 (单位:元)与销售单价
(单位:元)与销售单价 (单位:元/个)之间的函数关系式;
(单位:元/个)之间的函数关系式;(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点E在边AB上,AE=1,若点P为对角线BD上的一个动点,则△PAE周长的最小值是( )
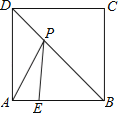
A.3B.4C.5D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民使用自来水按月收费,标准如下:
①若每户月用水不超过
 ,按
,按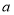 元/
元/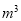 收费;
收费;②若超过
 ,但不超过
,但不超过 ,则超过的部分按
,则超过的部分按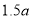 元/
元/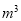 收费,未超过
收费,未超过 部分按①标准收费;
部分按①标准收费;③若超过
 ,超过的部分按
,超过的部分按 元/
元/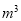 收费,未超过
收费,未超过 部分按②标准收费;
部分按②标准收费;(1)若用水
 ,应交水费______元;(用含
,应交水费______元;(用含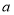 的式子表示)
的式子表示)(2)小明家上个月用水
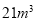 ,交水费
,交水费 元,求
元,求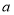 的值;
的值;(3)在(2)的条件下,小明家七、八两个月共交水费
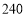 元,七月份用水
元,七月份用水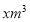 超过
超过 ,但不足
,但不足 ,八月份用水
,八月份用水 超过
超过 ,当
,当 均为整数时,求
均为整数时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
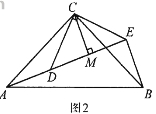
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.

(3)解决问题如图3,在正方形ABCD中,CD=
 .若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
.若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是________.

相关试题

