【题目】计算:
(1)9×(﹣ ![]() )2+
)2+ ![]() ﹣|﹣3|
﹣|﹣3|
(2)![]()
(3)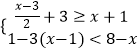
,并将不等式组的解集在所给数轴上表示出来.
参考答案:
【答案】
(1)解:9×(﹣ ![]() )2+
)2+ ![]() ﹣|﹣3|
﹣|﹣3|
=9× ![]() +2﹣3
+2﹣3
=1+2﹣3
=0
(2)解: ![]()
①×3+②得:10x=20,即x=2,
把x=2代入①得:y=﹣1,
则方程组的解为 ![]()
(3)解: 
解不等式①得:x≤1,
解不等式②得:x>﹣2,
原不等式红的解为:﹣2<x≤1.
不等式组的解集在数轴上表示:
 .
.
【解析】
①分别进行,开平方,绝对值的化简等运算,然后计算乘法,最后合并.
②方程组利用加减消元法求出.
③先求出不等式组中每一个不等式的解集,在求出他们的公共部分就是不等式组的解集.
【考点精析】利用解二元一次方程组和不等式的解集在数轴上的表示对题目进行判断即可得到答案,需要熟知二元一次方程组:①代入消元法;②加减消元法;不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角△ABC中,边BC长为12,高AD长为8.
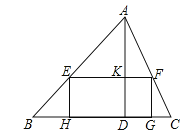
(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.
①求
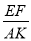 的值;
的值;②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值;
(2)若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.(
 取1.73)
取1.73)(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DE上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
(1)求sin∠EAC的值.
(2)求线段AH的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程组
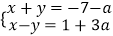 的解中,x为非正数,y为负数.
的解中,x为非正数,y为负数.
(1)求a的取值范围;
(2)化简|a﹣3|+|a+2|. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查市场上某品牌方便面的色素含量是否符合国家标准,工作人员在超市里随机抽取了某品牌的方便面进行检验.图1和图2是根据调查结果绘制的两幅不完整的统计图,其中A、B、C、D分别代表色素含量为0.05%以下、0.05%~0.1%、0.1%~0.15%、0.15%以上,图1的条形图表示的是抽查的方便面中色素含量分布的袋数,图2的扇形图表示的是抽查的方便面中色素的各种含量占抽查总数的百分比.请解答以下问题:
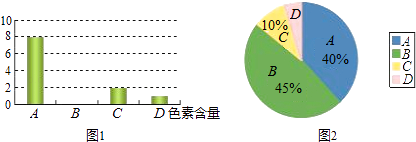
(1)本次调查一共抽查了多少袋方便面?
(2)将图1中色素含量为B的部分补充完整;
(3)图2中的色素含量为D的方便面所占的百分比是多少?
(4)若色素含量超过0.15%即为不合格产品,某超市这种品牌的方便面共有10000袋,那么其中不合格的产品有多少袋? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B.C在同一水平地面上.
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(
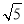 ≈2.236,结果精确到0.1m)
≈2.236,结果精确到0.1m)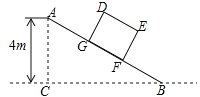
相关试题

