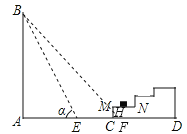
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.(![]() 取1.73)
取1.73)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.

参考答案:
【答案】(1)17.3;(2)当α=45°时,小猫仍可以晒到太阳.
【解析】
试题分析:(1)在Rt△ABE中,由tan60°=![]() ,即可求出AB=10tan60°=17.3米;
,即可求出AB=10tan60°=17.3米;
(2)假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.由∠BFA=45°,可得AF=AB=17.3米,那么CF=AF﹣AC=0.1米,CH=CF=0.1米,所以大楼的影子落在台阶MC这个侧面上,故小猫仍可以晒到太阳.
试题解析:(1)当α=60°时,在Rt△ABE中,∵tan60°=![]() ,∴AB=10tan60°=
,∴AB=10tan60°=![]() ≈10×1.73=17.3米.即楼房的高度约为17.3米;
≈10×1.73=17.3米.即楼房的高度约为17.3米;
(2)当α=45°时,小猫仍可以晒到太阳.理由如下:
假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.
∵∠BFA=45°,∴tan45°=![]() =1,此时的影长AF=AB=17.3米,∴CF=AF﹣AC=17.3﹣17.2=0.1米,∴CH=CF=0.1米,∴大楼的影子落在台阶MC这个侧面上,∴小猫仍可以晒到太阳.
=1,此时的影长AF=AB=17.3米,∴CF=AF﹣AC=17.3﹣17.2=0.1米,∴CH=CF=0.1米,∴大楼的影子落在台阶MC这个侧面上,∴小猫仍可以晒到太阳.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,2018年10月1日全国共接待了国内游客122000000次,用科学计数法表示122000000为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:3﹣2×(﹣1)=( )
A.5
B.1
C.﹣1
D.6 -
科目: 来源: 题型:
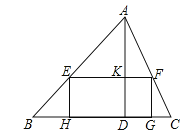
查看答案和解析>>【题目】已知锐角△ABC中,边BC长为12,高AD长为8.
(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.
①求
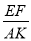 的值;
的值;②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值;
(2)若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DE上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
(1)求sin∠EAC的值.
(2)求线段AH的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)9×(﹣ )2+
)2+ 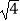 ﹣|﹣3|
﹣|﹣3|
(2)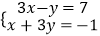
(3)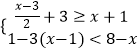
,并将不等式组的解集在所给数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程组
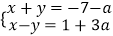 的解中,x为非正数,y为负数.
的解中,x为非正数,y为负数.
(1)求a的取值范围;
(2)化简|a﹣3|+|a+2|.
相关试题

