【题目】如图,在△ABC中,D是BC边上的点(不与点B,C重合),连结AD

(1)如图1,当点D是BC边上的中点时,则S△ABD:S△ACD=_________(直接写出答案)
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,S△ABD:S△ACD=_________ (用含m,n的代数式表示).
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连结BE,如果AC=2,AB=4,S△BDE =6,求△ABC的面积.
参考答案:
【答案】(1)1:1;(2)m∶n;(3)9
【解析】
(1)过A作AE⊥BC于E,根据三角形面积公式求出即可;
(2)过D作DE⊥AB于E,DF⊥AC于F,根据角平分线性质求出DE=DF,根据三角形面积公式求出即可;
(3)根据已知和(1)(2)的结论求出△ABD和△ACD的面积,即可求出答案.
解:(1)过A作AE⊥BC于E,
∵点D是BC边上的中点,
∴BD=DC,
∴SABD:S△ACD=(![]() ×BD×AE):(
×BD×AE):(![]() ×CD×AE)=1:1,
×CD×AE)=1:1,
故答案为:1:1;

(2)过D作DE⊥AB于E,DF⊥AC于F,
∵AD为∠BAC的角平分线,
∴DE=DF,
∵AB=m,AC=n,
∴SABD:S△ACD=(![]() ×AB×DE):(
×AB×DE):(![]() ×AC×DF)=m:n;
×AC×DF)=m:n;

(3)∵AD=DE,
∴由(1)知:S△ABD:S△EBD=1:1,
∵S△BDE=6,
∴S△ABD=6,
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知:S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=3+6=9,
故答案为:9.

-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小王某天下午营运全是在南北走向的公路上进行的。如果向南记作“
 ”,向北记作“
”,向北记作“ ”他这天下午行车情况如下:(单位:千米;每次行车都有乘客)
”他这天下午行车情况如下:(单位:千米;每次行车都有乘客) ,
,  ,
,  ,
, 
 ,
, 


请回答:
(
 )小王将最后一名乘客送到目的地时,小王在下午出车的出发地的什么方向?距下午出车的出发地多远?
)小王将最后一名乘客送到目的地时,小王在下午出车的出发地的什么方向?距下午出车的出发地多远?(
 )若小王的出租车每千米耗油
)若小王的出租车每千米耗油 升,不计汽车的损耗,共耗油多少升?
升,不计汽车的损耗,共耗油多少升?(
 )若规定每敞车的起步价是
)若规定每敞车的起步价是 无,且每趟车3千米以内(含3千米)只收起步价;若超过3千米,除收起步价外,超过的每千米还需收
无,且每趟车3千米以内(含3千米)只收起步价;若超过3千米,除收起步价外,超过的每千米还需收 元钱,那么小王这天下午收到乘客所给车费共多少元?
元钱,那么小王这天下午收到乘客所给车费共多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图,△ABC中,AB=AC,且∠A=36°.

(1)在图中用尺规作边AB的垂直平分线交AC于D,连接BD(保留作图痕迹,不写作法).
(2)请问△BDC是不是黄金三角形,如果是,请给出证明,如果不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:在数轴上
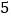 与
与 所对的两点之间的距离:
所对的两点之间的距离: ;
;在数轴上
 与
与 所对的两点之间的距离:
所对的两点之间的距离: ;
;在数轴上
 与
与 所对的两点之间的距离:
所对的两点之间的距离: ;
;在数轴上点
 、
、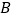 分别表示数
分别表示数 、
、 ,则
,则 、
、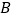 两点之间的距离
两点之间的距离 .
.请回答下列问题:
(
 )数轴上表示
)数轴上表示 和
和 的两点之间的距离是__________.
的两点之间的距离是__________.数轴上表示数
 和
和 的两点之间的距离表示为__________.数轴上表示数__________和__________的两点之间的距离表示为
的两点之间的距离表示为__________.数轴上表示数__________和__________的两点之间的距离表示为 .
.(
 )七年级研究性学习小组在数学老师指导下,对式子进行探究:
)七年级研究性学习小组在数学老师指导下,对式子进行探究: .
.①请你在草稿纸上画出数轴,当表示数
 的点在
的点在 与
与 之间移动时,
之间移动时, 的值总是一个固定的值为:__________.(直接写出结果)
的值总是一个固定的值为:__________.(直接写出结果)②请你在草稿纸上画出数轴,要使
 ,数轴上满足条件的点表示的数字是:__________(直接写出结果).
,数轴上满足条件的点表示的数字是:__________(直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】某种小商品的成本价为10元/kg,市场调查发现,该产品每天的销售量w(kg)与销售价x(元/kg)有如下关系w=﹣2x+100,设这种产品每天的销售利润为y(元).
(1)求y与x之间的函数关系式;
(2)当售价定为多少元时,每天的销售利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.

(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.
相关试题

