【题目】如图1,在平面直角坐标系中,正方形OABC的顶点A和C分别在x轴和y轴正半轴上,点B坐标为(3,3),抛物线y=﹣x2+bx+c过点A、C,交x轴负半轴于点D,与BC边的另一个交点为E,抛物线的顶点为M,对称轴交x轴于点N.
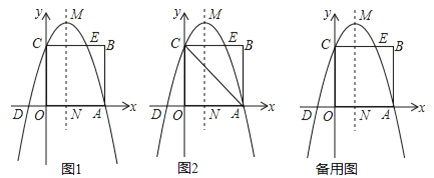
(1)求抛物线的函数关系式;
(2)点P在直线MN上,求当PE+PA的值最小时点P的坐标;
(3)如图2,探索在x轴是否存在一点F,使∠CFO=∠CDO﹣∠CAO?若存在,求点F的坐标;不存在,说明理由;
(4)将抛物线沿y轴方向平移m个单位后,顶点为Q,若QO平分∠CQN,求点Q的坐标.
参考答案:
【答案】(1)y=-x2+2x+3;(2)P(1,2)(3)F(6,0),(-6,0);(4)Q(1, ![]() ),(1,
),(1, ![]() )
)
【解析】试题分析:(1)由已知条件易得点A和点C的坐标,再利用待定系数法即可求得函数的解析式;(2)AC与对称轴的交点就是P,利用待定系数法求得AC的解析式,即可求得点P的坐标;(3)在y轴的正半轴上截取OH=OD=1,则H的坐标是(0,1),延长DH交AC于点G,则DG⊥AC,∠CDH=∠CDO﹣∠CAO,当F在x轴的负半轴上时,当∠CFO=∠CDH=∠CDO﹣∠CAO时,则△CFO∽△CDG,根据相似三角形的对应边的比相等即可求得OF的长,则F的坐标即可求得,然后根据对称性求得F在x轴的正半轴时的坐标;
(4)当抛物线沿y轴的正半轴移动时,Q的横坐标是1,QO平分∠CQN,则CQ=OC,利用勾股定理即可求得Q的纵坐标;同理求得抛物线沿y轴的负半轴移动时Q的坐标.
试题解析: 解:(1)∵四边形OABC是正方形,B的坐标是(3,3),
∴A的坐标是(3,0),C的坐标是(0,3).
根据题意得![]() ,
,
解得:![]() ,
,
则二次函数的解析式是y=﹣x2+2x+3;
(2)设直线AC的解析式是y=ax+b,
![]() ,
,
解得:![]() ,
,
则直线AC的解析式是y=﹣x+3,
当x=1时,y=﹣1+3=2,
则P的坐标是(1,2);
(3)在y=﹣x2+2x+3中令y=0,则﹣x2+2x+3=0,解得x=﹣1或x=3.
则D的坐标是(﹣1,0)A的坐标是(3,0).
在y轴的正半轴上截取OH=OD=1,则H的坐标是(0,1),延长DH交AC于点G,则DG⊥AC;
∵直角△ODF中,OH=OD,
∴∠HDO=45°,
同理,∠CAO=45°,
∴∠HDO=∠CAO.则∠CDH=∠CDO﹣∠CAO.
当F在x轴的负半轴上时,
设DG的解析式是y=ex+f,则![]() ,
,
解得![]() ,则DG的解析式是y=x+1.
,则DG的解析式是y=x+1.
根据题意得:![]() ,
,
解得:![]() ,
,
则G的坐标是(1,2).
则DG=![]() ,CD=
,CD=![]() ,CG=
,CG=![]() .
.
当∠CFO=∠CDH=∠CDO﹣∠CAO时,△CFO∽△CDG,
则![]() ,即
,即![]() ,解得:OF=6,
,解得:OF=6,
则F的坐标是(﹣6,0).
根据对称性可得当F在x轴的正半轴上时F的坐标是(6,0);
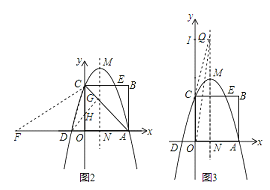
(4)当抛物线沿y轴的正半轴移动时,如图3,
设Q的坐标是(1,n).作QI⊥y轴于点I.则IQ=1,IC=n﹣3,
则QO平分∠CQN,则CQ=OC=3,12+(n﹣3)2=32,
解得:n=3+2![]() ,
,
则Q的坐标是(1,3+2![]() );
);
同理,当抛物线沿y轴的负方向移动时Q的坐标是(1,3﹣2![]() ).
).
总之,Q的坐标是(1,3+2![]() )或(1,3﹣2
)或(1,3﹣2![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若任意一个三位数t的百位数字为a,十位数字为b,个位数字为c,那么可将这个三位数表示为t=
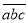 (a≠0),且满足t=100a+10b+c,我们把三位数各位上的数字的乘积叫做原数的积数,记为P(t).重新排列一个三位数各位上的数字,必可以得到一个最大的三位数和一个最小的三位数,此最大三位数与最小三位数之差叫做原数的差数,记为F(t),例如:264的积数P(264)=48,差数F(264)=642﹣246=396.
(a≠0),且满足t=100a+10b+c,我们把三位数各位上的数字的乘积叫做原数的积数,记为P(t).重新排列一个三位数各位上的数字,必可以得到一个最大的三位数和一个最小的三位数,此最大三位数与最小三位数之差叫做原数的差数,记为F(t),例如:264的积数P(264)=48,差数F(264)=642﹣246=396.(1)根据以上材料:F(258)= ;
(2)若一个三位数t=
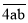 ,且P(t)=0,F(t)=135,求这个三位数.
,且P(t)=0,F(t)=135,求这个三位数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB=
 ,E是弧AB的中点,求EGED的值.
,E是弧AB的中点,求EGED的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD为□ABCD的对角线,按要求完成下列各题.

(1)用直尺和圆规作出对角线BD的垂直平分线交AD于点E,交BC于点F,垂足为O.(保留作图痕迹,不要求写作法)
(2)在(1)的基础上,连接BE和DF.求证:四边形BFDE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数
 ,当
,当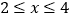 时,函数有最大值5.
时,函数有最大值5.(1)求此二次函数图象与坐标轴的交点;
(2)将函数
 图象x轴下方部分沿x轴向上翻折,得到的新图象与直线
图象x轴下方部分沿x轴向上翻折,得到的新图象与直线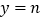 恒有四个交点,从左到右,四个交点依次记为
恒有四个交点,从左到右,四个交点依次记为 ,当以
,当以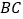 为直径的圆与
为直径的圆与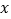 轴相切时,求
轴相切时,求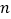 的值.
的值.(3)若点
 是(2)中翻折得到的抛物线弧部分上任意一点,若关于m的一元二次方程
是(2)中翻折得到的抛物线弧部分上任意一点,若关于m的一元二次方程 恒有实数根时,求实数k的最大值.
恒有实数根时,求实数k的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连结AC,将△ACE沿AC翻转得到△ACF,直线FC与直线AB相交于点G.
(1)求证:FG是⊙O的切线;
(2)若B为OG的中点,CE=
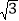 ,求⊙O的半径长;
,求⊙O的半径长;(3)①求证:∠CAG=∠BCG;
②若⊙O的面积为4π,GC=2
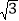 ,求GB的长.
,求GB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两家汽车销售公司根据近几年的销售量分别制作了如图所示的统计图,从2014~2018年,这两家公司中销售量增长较快的是_____公司(填“甲”或“乙”).

相关试题

