【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

参考答案:
【答案】OM=15米;MN=2米.
【解析】
作AE⊥OM,BF⊥OM,首先得出△AOE≌△OBF(AAS),进而得出CD的长,进而求出OM,MN的长即可.
解:
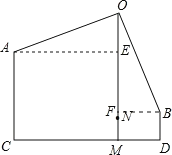
作AE⊥OM,BF⊥OM,
∵∠AOE+∠BOF=∠BOF+∠OBF=![]() ,
,
∴∠AOE=∠OBF,
在△AOE和△OBF中,
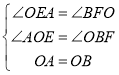 ,
,
∴△AOE≌△OBF(AAS),
∴OE=BF,AE=OF,
即OE+OF=AE+BF=CD=17(m),
∵EF=EMFM=ACBD=103=7(m),
∴2EO+EF=17,
则2×EO=10,
所以OE=5m,OF=12m,
所以OM=OF+FM=15m,
又因为由勾股定理得ON=OA=13,
所以MN=1513=2(m).
答:旗杆的高度OM为15米,玛丽在荡绳索过程中离地面的最低点的高度MN为2米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半⊙O中,AB是直径,点D是⊙O上一点,点C是
 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQCB,其中结论正确的是____.
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQCB,其中结论正确的是____.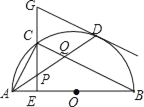
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一张三角形纸片
 如图甲
如图甲 ,其中
,其中 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为 如图乙
如图乙 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为 如图丙
如图丙 原三角形纸片ABC中,
原三角形纸片ABC中, 的大小为______
的大小为______

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC中,AB=AC,∠ACB=72°,

(1)若BD⊥AC于D,求∠ABD的度数;
(2)若CE平分∠ACB,求证:AE=BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A. B. C的坐标分别为(1,0)、(2,3)、(3,1).

(1)作出△ABC关于x轴对称的△A1 B1 C1,并写出B1的坐标:B1(___,___)
(2)在y轴上找一点D,使得BD+DA的值最小,D点的坐标______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为
中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为 ,点B在x负半轴上,反比例函数
,点B在x负半轴上,反比例函数 的图象经过C点.
的图象经过C点.(1)求该反比例函数的解析式;
(2)当函数值
 >-2时,请直接写出自变量x的取值范围;
>-2时,请直接写出自变量x的取值范围;(3)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.

相关试题

