【题目】已知矩形ABCD,点E在AD边上,DE>AE,连接BE,将△ABE沿着BE翻折得到△BFE,射线EF交BC于G,若点G为BC的中点,FG=1,DE=6,则AE的长 . 
参考答案:
【答案】4
【解析】解:设AE=EF=x,
∵DE=6,FG=1,
∴AD=x+6=BC,EG=x+1,
又∵G为BC的中点,
∴BG= ![]() BC=
BC= ![]() ,
,
由折叠可得,∠AEB=∠GEB,
由AD∥BC,可得∠AEB=∠GBE,
∴∠GEB=∠GBE,
∴EG=BG,
∴x+1= ![]() ,
,
解得x=4,
即AE=4,
所以答案是:4.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
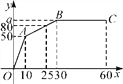
查看答案和解析>>【题目】“和谐号”火车从车站出发,在行驶过程中速度y(单位:m/s)与时间x(单位:s)的关系如图所示,其中线段BC∥x轴.请根据图象提供的信息解答下列问题:
(1)当0≤x≤10,求y关于x的函数解析式;
(2)求C点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用直角边分别为3和4的两个直角三角形拼成一个平行四边形(非矩形),所得的平行四边形的周长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是BC边上的中线,AE是BC边上的高.
(1)若∠ACB=100°,求∠CAE的度数;
(2)若S△ABC=12,CD=4,求高AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】图1、图2分别是7×6的网格,网格中的每个小正方形的边长均为1,点A、B在小正方形的顶点上.

(1)在图1中确定点C(点C在小正方形的顶点上),要求以A、B、C为顶点的三角形为锐角等腰三角形,画出此三角形(画出一个即可);
(2)在图2中确定点D(点D在小正方形的顶点上),要求以A、B、D为顶点的三角形是以AB为斜边的直角三角形,画出此三角形(画出一个即可),并直接写出此三角形的周长 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.
 B.3 C.1 D.
B.3 C.1 D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AD是BC边上的高,∠BDE=∠CDF=30°,在下列结论中:①△ABD≌△ACD;②2DE=2DF=AD;③△ADE≌△ADF;④4BE=4CF=AB.正确的个数是( )

A. 1 B. 2 C. 3 D. 4
相关试题

