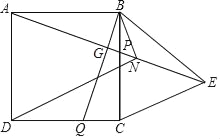
【题目】如图,在正方形ABCD中,点P、Q分别为BC、CD边上一点,且BP=CQ=![]() BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN=
BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN=![]() ,则CE的长为_____.
,则CE的长为_____.
参考答案:
【答案】![]()
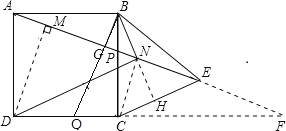
【解析】分析:首先得出∠AGB=90°,过点D作DM⊥AN于M,根据五点共圆的性质得出Rt△DMN,Rt△BGN都是等腰直角三角形,然后根据DN的长度得出正方形的边长,根据△ABP的等积法得出BG的长度,然后根据△BGP和△CNP相似得出CN的长度,最后根据等腰直角三角形的性质得出CE的长度.
详解:∵BP=CQ,则△ABP≌△BCQ,∴∠AGB=90°,
连接CN,延长BN交CE于H. 过点D作DM⊥AN于M,
∴Rt△ADM≌Rt△ABG,DM=AG, ∵BN平分∠CBE,∴CH=HE,
∵∠CBN=∠EBN,BE=BC,BN=BN, ∴△BCN≌△BEN,
∴CN=NE,△CEN是等腰三角形,
延长AE交DC延长线于F,则有:∠BAG=∠BEG=∠CFE=∠BCN,
A,B,C,D,N五点共圆,∠AND=∠BNG=45°[AB弦所对圆周角=45°]
Rt△DMN,Rt△BGN都是等腰直角三角形,
∵DN=![]() , ∴AB=MN=
, ∴AB=MN=![]() ,根据△ABP的等积法可得:BG=
,根据△ABP的等积法可得:BG=![]() ,
,
∵△BGP∽△CNP,则CN=2BG=![]() ,则CE=
,则CE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走260米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.则大楼AB的高度约为( )米.
(参考书据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

A. 170 B. 175 C. 180 D. 190
-
科目: 来源: 题型:
查看答案和解析>>【题目】若数a使关于x的分式方程
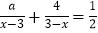 的解为正数,使关于y的不等式组
的解为正数,使关于y的不等式组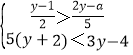 无解,则所有满足条件的整数a的值之积是( )
无解,则所有满足条件的整数a的值之积是( )A. 360 B. 90 C. 60 D. 15
-
科目: 来源: 题型:
查看答案和解析>>【题目】具备下列条件的两个三角形,可以证明它们全等的是( ).
A.一边和这一边上的高对应相等B.两边和第三边上的中线对应相等
C.两边和其中一边的对角对应相等D.直角三角形的斜边对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(-2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是( )

A. (-2,0) B. (0,0) C. (2,0) D. (4,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC中,∠ACB=90°,AC=BC,点E是BC上一点,连接AE.
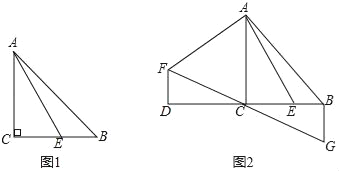
(1)如图1,当∠BAE=15°,CE=
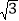 时,求AB的长.
时,求AB的长.(2)如图2,延长BC至D,使DC=BC,将线段AE绕点A顺时针旋转90°得线段AF,连接DF,过点B作BG⊥BC,交FC的延长线于点G,求证:BG=BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )

A. 10cm B. 12cm C. 15cm D. 17cm
相关试题

