【题目】在平面直角坐标系xOy中,点M的坐标为(x1,y1),点N的坐标为(x2,y2),且x1≠x2,y1≠y2,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”.
(1)已知点A(2,0),B(0,2![]() ),则以AB为边的“坐标菱形”的最小内角为 ;
),则以AB为边的“坐标菱形”的最小内角为 ;
(2)若点C(1,2),点D在直线y=5上,以CD为边的“坐标菱形”为正方形,求直线CD 表达式;
(3)⊙O的半径为![]() ,点P的坐标为(3,m).若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
,点P的坐标为(3,m).若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
参考答案:
【答案】(1)60°;(2)y=x+1或y=﹣x+3;(3)1≤m≤5或﹣5≤m≤﹣1
【解析】分析:(1)根据定义建立以AB为边的“坐标菱形”,由勾股定理求边长AB=4,可得30度角,从而得最小内角为60°;
(2)先确定直线CD与直线y=5的夹角是45°,得D(4,5)或(﹣2,5),易得直线CD的表达式为:y=x+1或y=﹣x+3;
(3)分两种情况:
①先作直线y=x,再作圆的两条切线,且平行于直线y=x,如图3,根据等腰直角三角形的性质分别求P'B=BD=1,PB=5,写出对应P的坐标;
②先作直线y=﹣x,再作圆的两条切线,且平行于直线y=﹣x,如图4,同理可得结论.
详解:(1)∵点A(2,0),B(0,2![]() ),∴OA=2,OB=2
),∴OA=2,OB=2![]() .在Rt△AOB中,由勾股定理得:AB=
.在Rt△AOB中,由勾股定理得:AB=![]() =4,∴∠ABO=30°.
=4,∴∠ABO=30°.
∵四边形ABCD是菱形,∴∠ABC=2∠ABO=60°.
∵AB∥CD,∴∠DCB=180°﹣60°=120°,∴以AB为边的“坐标菱形”的最小内角为60°.
故答案为:60°;
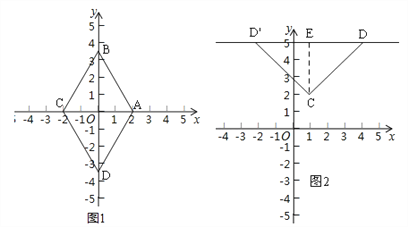
(2)如图2.
∵以CD为边的“坐标菱形”为正方形,∴直线CD与直线y=5的夹角是45°.
过点C作CE⊥DE于E,∴D(4,5)或(﹣2,5),∴直线CD的表达式为:y=x+1或y=﹣x+3;
(3)分两种情况:
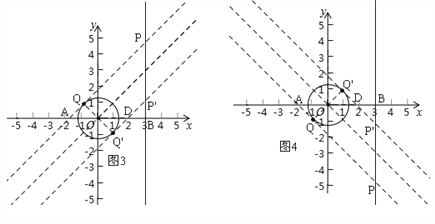
①先作直线y=x,再作圆的两条切线,且平行于直线y=x,如图3.
∵⊙O的半径为![]() ,且△OQ'D是等腰直角三角形,∴OD=
,且△OQ'D是等腰直角三角形,∴OD=![]() OQ'=2,∴P'D=3﹣2=1.
OQ'=2,∴P'D=3﹣2=1.
∵△P'DB是等腰直角三角形,∴P'B=BD=1,∴P'(0,1),同理可得:OA=2,∴AB=3+2=5.
∵△ABP是等腰直角三角形,∴PB=5,∴P(0,5),∴当1≤m≤5时,以QP为边的“坐标菱形”为正方形;
②先作直线y=﹣x,再作圆的两条切线,且平行于直线y=﹣x,如图4.
∵⊙O的半径为![]() ,且△OQ'D是等腰直角三角形,∴OD=
,且△OQ'D是等腰直角三角形,∴OD=![]() OQ'=2,∴BD=3﹣2=1.
OQ'=2,∴BD=3﹣2=1.
∵△P'DB是等腰直角三角形,∴P'B=BD=1,∴P'(0,﹣1),同理可得:OA=2,∴AB=3+2=5.
∵△ABP是等腰直角三角形,∴PB=5,∴P(0,﹣5),∴当﹣5≤m≤﹣1时,以QP为边的“坐标菱形”为正方形;
综上所述:m的取值范围是1≤m≤5或﹣5≤m≤﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,CD⊥BC于点C,交∠ABC的平分线于点D,AE平分∠BAC交BD于点E,过点E作EF∥BC交AC于点F,连接DF.
(1)补全图1;
(2)如图1,当∠BAC=90°时,
①求证:BE=DE;
②写出判断DF与AB的位置关系的思路(不用写出证明过程);
(3)如图2,当∠BAC=α时,直接写出α,DF,AE的关系.
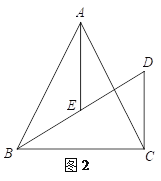
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上A. B两点对应的数分别为4和2,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A.点B的距离相等,写出点P对应的数;
(2)数轴上是否存在点P,使点P到点A. 点B的距离之和为10?若存在,求出x的值;若不存在,请说明理由;
(3)若点A点B和点P(点P在原点)同时向右运动,它们的速度分别为2、1、1个长度单位/分,问:多少分钟后P点到点A点B的距离相等?(直接写出结果)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图像回答下列问题:
(1)小华在体育馆锻炼了_____分钟;
(2)体育馆离文具店______千米;
(3)小华从家跑步到体育馆,从文具店散步回家的速度分别是多少千米/分钟?

-
科目: 来源: 题型:
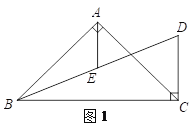
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)若AC=BF,求∠ABD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线,分别交AD,AC于P,Q两点;(要求:尺规作图,保留作图痕迹,不写作法)
(2)证明AP=AQ.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“五四”青年节期间,校团委对团员参加活动情况进行表彰,计划分为优秀奖和贡献奖,为此联系印刷公司设计了两种奖状,A,B两家公司都为学校提出了相同规格和单价的两种奖状,其中优秀奖的奖状6元/张,贡献奖的奖状5元/张,经过协商,A公司的优惠条件是:两种奖状都打八折,但要收制版费50元;B公司的优惠条件是:两种奖状都打九折;根据学校要求,优秀奖的个数是贡献奖的2倍还多10个,如果设贡献奖的个数是x个.
(1)分别写出校团委购买A,B两家印刷厂所需要的总费用y1(元)和y2(元)与贡献奖个数x之间的函数关系式;
(2)校团委选择哪家印刷公司比较合算?请说明理由.
相关试题

