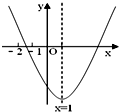
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:①b2﹣4ac>0 ②a>0 ③b>0 ④c>0 ⑤9a+3b+c<0,则其中结论正确的个数是( )
A、2个B、3个
C、4个D、5个
参考答案:
【答案】B
【解析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据抛物线与x轴交点及x=1时二次函数的值的情况进行推理,进而对所得结论进行判断.
解答:解:①根据图示知,二次函数与x轴有两个交点,所以△=b2-4ac>0;故①正确;
②根据图示知,该函数图象的开口向上,
∴a>0;
故②正确;
③又对称轴x=-![]() =1,
=1,
∴![]() <0,
<0,
∴b<0;
故本选项错误;
④该函数图象交于y轴的负半轴,
∴c<0;
故本选项错误;
⑤根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称点是(3,0);
当x=-1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故⑤正确.
所以①②⑤三项正确.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的折线是某个函数的图象,根据图象解答下列问题.
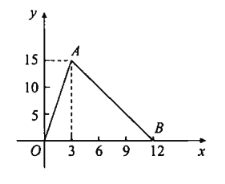
(1)写出自变量x的取值范围:__________,函数值y的取值范围:__________;
(2)求这个分段函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ACD和△BCE中, AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为( )
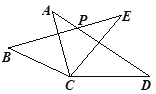
A.110°B.125°C.130°D.155°
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象如图所示,下列结论:
的图象如图所示,下列结论:①
 ;②
;② ;③
;③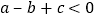 ;④
;④ ;⑤
;⑤ ;⑥当
;⑥当 时,
时, 随
随 的增大而增大.
的增大而增大.其中正确的说法有________(写出正确说法的序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC底边BC的长为4,面积为12,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边的中点,M为线段EF上一个动点,则△BDM的周长的最小值为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
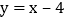 与
与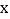 轴、
轴、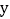 轴分别交于
轴分别交于 、
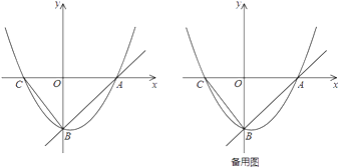
、 两点,抛物线
两点,抛物线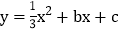 经过
经过 、
、 两点,与
两点,与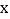 轴的另一个交点为
轴的另一个交点为 ,连接
,连接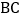 .
.
(1)求抛物线的解析式及点
 的坐标;
的坐标;(2)点
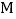 在抛物线上,连接
在抛物线上,连接 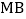 ,当
,当 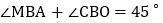 时,求点
时,求点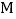 的坐标;
的坐标;(3)点
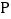 从点
从点 出发,沿线段
出发,沿线段 由
由 向
向 运动,同时点
运动,同时点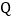 从点
从点 出发,沿线段
出发,沿线段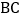 由
由 向
向 运动,
运动, 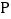 、
、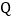 的运动速度都是每秒
的运动速度都是每秒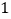 个单位长度,当
个单位长度,当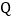 点到达
点到达 点时,
点时,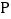 、
、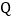 同时停止运动,试问在坐标平面内是否存在点
同时停止运动,试问在坐标平面内是否存在点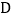 ,使
,使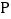 、
、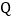 运动过程中的某一时刻,以
运动过程中的某一时刻,以 、
、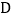 、
、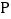 、
、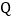 为顶点的四边形为菱形?若存在,直接写出点
为顶点的四边形为菱形?若存在,直接写出点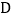 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
相关试题

