【题目】已知数轴上两点 A、B 所表示的数分别为 a 和 b,且满足|a+3|+(b-9)2018=0,O 为原点.
(1) 试求 a 和 b 的值
(2) 点 C 从 O 点出发向右运动,经过 3 秒后点 C 到 A 点的距离是点 C 到 B 点距离的 3 倍,求点 C 的运动速 度?
(3) 点 D 以 1 个单位每秒的速度从点 O 向右运动,同时点 P 从点 A 出发以 5 个单位每秒的速度向左运动, 点 Q 从点 B 出发,以 20 个单位每秒的速度向右运动.在运动过程中,M、N 分别为 PD、OQ 的中点,问![]() 的值是否发生变化,请说明理由.
的值是否发生变化,请说明理由.
参考答案:
【答案】(1)a=-3,b=9;(2)2或5.(3)不发生变化;理由见解析.
【解析】
(1)根据非负数的性质求得a、b的值即可;(2)设C速度为x,则3秒后C点所表示的数为3x,根据数轴上两点之间的距离列方程即可得出答案;(3)设运动时间为t,根据速度可求出t秒时P、D、Q、M、N的位置,求出PQ、OD、MN的距离,进而求出![]() 的值即可得答案.
的值即可得答案.
(1)∵|a+3|+(b-9)2018=0,
∴a+3=0,b-9=0,
解得:a=-3,b=9;
(2)设C速度为x,则3秒后C点所表示的数为3x,
∴∣AC∣=3∣BC∣,即∣3x-(-3)∣=3∣9-3x∣,
解得:x=2或x=5,
故C的速度为:2或5.
(3)不发生变化;理由如下:
设运动时间为t,根据题意得:
P点的位置为:-3-5t ,
D点的位置为:t ,
Q点的位置为:9+20t,
M点的位置为:t-![]() =
=![]() ,
,
N点的位置为:![]() ,
,
∴PQ=9+20t-(-3-5t)=12+25t;OD =t;MN=![]() -
-![]() =6+12t;
=6+12t;
∴![]() =
=![]() =2,
=2,
故![]() 的值不发生变化.
的值不发生变化.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为E、F,点O为AC的中点.
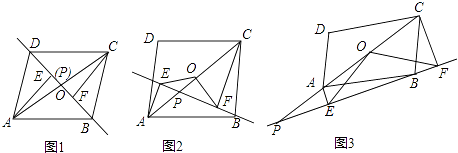
(1)当点P与点O重合时如图1,求证:OE=OF
(2)直线BP绕点B逆时针方向旋转,当点P在对角线AC上时,且∠OFE=30°时,如图2,猜想线段CF、AE、OE之间有怎样的数量关系?并给予证明.
(3)当点P在对角线CA的延长线上时,且∠OFE=30°时,如图3,猜想线段CF、AE、OE之间有怎样的数量关系?直接写出结论即可. -
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:
(1).先化简,再求值:3a2+(4a2-2a-1)-2(3a2-a+1),其中a1

(2). A=3a2+6ab-b2,B=2b2-5ab+a2,C=-4a2-ab+b2,先化简,再求值:A-[B-(A-B+3C)]-(A-B),其中 a=-0.2,b=-0.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,∠ABC=2∠C,BE平分∠ABC交AC于E,AD⊥BE于D,下列结论:①AC﹣BE=AE;②点E在线段BC的垂直平分线上;③∠DAE=∠C;④BC=4AD,其中正确的有( )
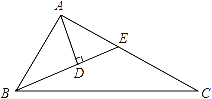
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂一周计划生产1 400辆自行车,平均每天生产200辆.由于各种原因,实际上每天的生产量与计划量相比有出入.表是某周的生产情况(增产为正,减产为负):
星期
一
二
三
四
五
六
日
增减
+5
﹣2
﹣4
+13
﹣10
+16
﹣9
(1)根据记录的数据可知该厂星期五生产自行车 辆;
(2)产量最多的一天比产量最少的一天多生产了 辆自行车;
(3)根据记录的数据可知该厂本周实际生产自行车 辆;
(4)该厂实行计件工资制,每生产一辆得60元,超额完成则每辆奖15元,少生产一辆则扣15元,那么该厂工人这一周的工资总额是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )
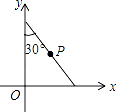
A.(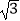 ,1)
,1)
B.(1,﹣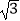 )
)
C.(2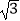 ,﹣2)
,﹣2)
D.(2,﹣2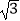 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为4个等边三角形,D为AB边的中点,以CD为直径画圆,则图中阴影部分的面积为(结果保留π).
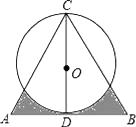
相关试题

