【题目】x= 3和x = - 6中, 是方程x - 3(x + 2) = 6的解.
参考答案:
【答案】x = - 6
【解析】解方程x - 3(x + 2) = 6,
去分母得:x-3x-6=6,
合并同类项得:-2x-6=6,
移项得:-2x=12,
系数化为1得:x=-6
【考点精析】认真审题,首先需要了解解一元一次方程的步骤(先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知ABCD的周长为8 cm,∠B=30°,若边长AB为x cm.
(1)写出ABCD的面积y(cm2)与x(cm)的函数关系式,并求自变量x的取值范围.
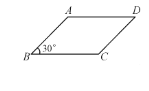
(2)当x取什么值时,y的值最大?并求出最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如下表(单位:秒):
编号
类型
一
二
三
四
五
六
七
八
九
十
甲种电子钟
1
-3
-4
4
2
-2
2
-1
-1
2
乙种电子钟
4
-3
-1
2
-2
1
-2
2
-2
1
(1) 计算甲、乙两种电子钟走时误差的平均数;
(2) 计算甲、乙两种电子钟走时误差的方差;
(3) 根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).
(1)当t为何值时,点F落在射线BC上;
(2)当线段CD将△AEF的面积二等分时,求t的值;
(3)求S与t的函数关系式;
(4)当S=17时,求t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程
(1)2x+5=3(x﹣1)
(2)4(7x﹣1)﹣6(5x+1)=24﹣3(3x+2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形两边长分别为4和6,则该三角形第三边的长可能是( )
A. 2 B. 9 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】明买了20本练习本,店主给他八折优惠,结果便宜1.6元,每本练习本的标价是元 。
相关试题

