【题目】如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).
(1)当t为何值时,点F落在射线BC上;
(2)当线段CD将△AEF的面积二等分时,求t的值;
(3)求S与t的函数关系式;
(4)当S=17时,求t的值.

参考答案:
【答案】(1)8(2)6(3)S= (4)5
(4)5
【解析】
试题分析:(1)由矩形的性质和等腰直角三角形的性质得出FH=8cm,再由运动得出FH=t,即可;
(2)由等腰直角三角形的性质得出斜边上的高也是中线,根据三角形的中线把三角形AEF面积平分,判断出点F在CD上,即可;
(3)分三种情况先利用矩形和运动的特点显示出三角形高,底边和梯形的上下底,高,再利用三角形和梯形的面积公式求解;
(4)先判断出面积是17时,运动时间在3<t≤6内,再直接代入函数关系式中,即可.
试题解析:(1)如图1,

过点F作FH⊥AD于H,
在矩形ABCD中,AB=8cm,BC=6cm,∠BAD=90°,
∵点F落在射线BC上,
∴FH=8cm,
∴t=8s,
(2)如图2,

∵△AEF是等腰直角三角形,
∴AE边上的高线也是该边的中线,
∴点F在边CD上时,CD将△AEF的面积二等分,
∵FD是直角三角形的斜边的直线,
∴由运动知,FD=AD=6=t,
∴t=6s,
(3)当0<t≤3时,如图3,
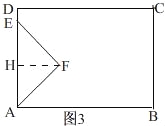
过点F作FH⊥AD,
由运动知,AE=2t,
∴FH=![]() AE=t,
AE=t,
∴S=![]() AE×FH=t2,
AE×FH=t2,
当3<t≤6时,如图4,

过点F作FH⊥AD,
由运动知,AE=2t,
∴DG=DE=2t﹣6,FH=t,DH=6﹣t,
∴S=![]() S△AEF+S梯形DHFG=
S△AEF+S梯形DHFG=![]() ×
×![]() AE×FH+
AE×FH+![]() (DG+FH)×DH=
(DG+FH)×DH=![]() ×
×![]() ×2t×t+
×2t×t+![]() (2t﹣6+t)×(6﹣t)=﹣t2+12t﹣18,
(2t﹣6+t)×(6﹣t)=﹣t2+12t﹣18,
当6<t≤8时,如图5,
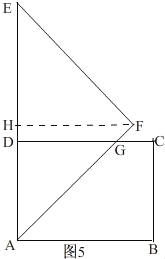
过点F作FH⊥AD,
∴DG=AD=6
∴S=![]() S△ADG=
S△ADG=![]() AD×GD=18;
AD×GD=18;
∴S=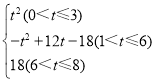 ,
,
(4)由函数关系式知,S=17的运动时间在3<t≤6中,
将S=17代入S=﹣t2+12t﹣18中,
∴﹣t2+12t﹣18=17,
∴t=7(舍)或t=5
∴当S=17时,t的值为5s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级一班数学老师对全班学生在模拟考试中A卷成绩进行统计后,制成如下的统计表:则该班学生A卷成绩的众数和中位数分别是( )
成绩(分)
80
82
84
86
87
90
人数
8
12
9
3
5
8
A. 82分,82分B. 82分,83分C. 80分,82分D. 82分,84分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知ABCD的周长为8 cm,∠B=30°,若边长AB为x cm.
(1)写出ABCD的面积y(cm2)与x(cm)的函数关系式,并求自变量x的取值范围.
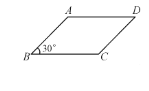
(2)当x取什么值时,y的值最大?并求出最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如下表(单位:秒):
编号
类型
一
二
三
四
五
六
七
八
九
十
甲种电子钟
1
-3
-4
4
2
-2
2
-1
-1
2
乙种电子钟
4
-3
-1
2
-2
1
-2
2
-2
1
(1) 计算甲、乙两种电子钟走时误差的平均数;
(2) 计算甲、乙两种电子钟走时误差的方差;
(3) 根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】x= 3和x = - 6中, 是方程x - 3(x + 2) = 6的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程
(1)2x+5=3(x﹣1)
(2)4(7x﹣1)﹣6(5x+1)=24﹣3(3x+2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形两边长分别为4和6,则该三角形第三边的长可能是( )
A. 2 B. 9 C. 10 D. 12
相关试题

