【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于y轴对称的△ABlCl;
(2)点P在x轴上,且点P到点B与点C的距离之和最小,直接写出点P的坐标为______.

参考答案:
【答案】(﹣![]() ,0)
,0)
【解析】
(1)根据网格结构找出点B,点C关于y轴对称的点B1,C1的位置,顺次连接各点即可;
(2)找出点C关于x轴的对称点C′,连接BC′,BC′与x轴的交点即可为所求作P点;根据对称性写出点C′的坐标,再根据点B,C′的坐标求出点P到CC′的距离,然后求出OP的长度即可得到点P的坐标.
(1)△ABC关于y轴对称的△ABlCl如图所示;

(2)如图,点P即为所求作的到点B与点C的距离之和最小,
点C′的坐标为(﹣1,﹣1),
∵点B(﹣2,2),∴点P到CC′的距离为![]() =
=![]() ,
,
∴OP=1+![]() =
=![]() ,点P(﹣
,点P(﹣![]() ,0).故答案为:(﹣
,0).故答案为:(﹣![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(b2)3(b3)4÷(﹣b5)3
(2)(
 )﹣1+(π﹣2018)0﹣(﹣1)2019
)﹣1+(π﹣2018)0﹣(﹣1)2019(3)(3﹣x)(﹣x+3)﹣x(x+1)
(4)(2a+b﹣5)(2a﹣b﹣5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.(1)如图,若点D为线段AC的中点,求证:AD=CE;
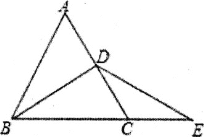
(2)如图,若点D为线段AC上任意一点,求证:AD=CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2﹣10x+16=0的两个根,且抛物线的对称轴是直线x=﹣2.

(1)求A,B,C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC,BC,若点E是线段AB上的一个动点(与点A,点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值?若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和直尺画图:
(1)补全△A′B′C′;
(2)作出△ABC的中线CD;
(3)画出BC边上的高线AE;
(4)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有 个.(注:格点指网格线的交点)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点D是△ABC所在平面内一点,连接AD、CD.
(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;
(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;
(3)如图3,在 (2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.

相关试题

