【题目】某市自来水公司为限制单位用水,每月只给某单位计划内用水300吨,计划内用水每吨收费3. 4元,超计划部分每吨按4. 6元收费.
(1)用代数式表示(所填结果需化简):
设用水量为![]() 吨,当用水量小于等于300吨,需付款 元;当用水量大于300吨,需付款 元.
吨,当用水量小于等于300吨,需付款 元;当用水量大于300吨,需付款 元.
(2)若某单位4月份缴纳水费1480元,则该单位用水多少吨?
(3)若某单位5、6月份共用水750吨(6月份用水量超过5月份),共交水费2790元,则该单位5、6月份各用水多少吨?
参考答案:
【答案】(1)3.4x ,4.6x-360 ;(2)400;(3)5月用水250t,6月用水500t
【解析】
(1)根据收费标准,找出当x≤300及x>300两种情况下需付款数额;
(2)求出用水300吨时缴纳的水费,比较后可得出该单位4月份用水超过300吨,根据(1)的结论可得出关于x的一元一次方程,解之即可得出结论;
(3)设该单位5月份用水y吨,则6月份用水(700-y)吨,分y≤300及y>300两种情况考虑:①当y≤300时,根据(1)的结论可得出关于y的一元一次方程,解之即可得出结论;②当y>300时,由6月份用水量超过5月份可得出y的取值范围,再求出两个月的水费,比较后可得知该情况不成立.综上即可得出结论.
(1)当x≤300时,需付款3.4x元;
当x>300时,需付款300×3.4+4.6(x-300)=(4.6x-360)元.
故答案是:3.4x;(4.6x-360).
(2)∵3.4×300=1020(元),1020<1480,
∴该单位4月份用水超过300吨.
根据题意得:4.6x-360=1480,
解得:x=400.
答:该单位4月份用水400吨.
(3)设该单位5月份用水y吨,则6月份用水(750-y)吨.
①当y≤300时,有3.4y+4.6(750-y)-360=2790,
解得:y=250,
700-y=750-250=500;
②当y>300时,∵6月份用水量超过5月份,
∴750-y>y,
∴300<y<375.
∵600×3.4+(750-600)×4.6=2730≠2790,
∴此种情况不成立.
答:该单位5月份用水250吨,6月份用水500吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某收费站在2小时内对经过该站的机动车统计如下:
类型
轿车
货车
客车
其他
数量(辆)
36
24
8
12
若有一辆机动车将经过这个收费站,利用上面的统计估计它是轿车的概率为( )
A.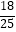
B.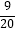
C.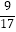
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.
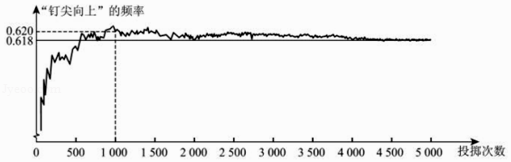
下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A.①
B.②
C.①②
D.①③ -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知A(-1,5),B(4,2),C(-1,0)三点.
(1)点A的对称点A′的坐标为(1,-5),点B关于x轴的对称点B′的坐标为________,点C关于y轴的对称点C′的坐标为________;
(2)求(1)中的△A′B′C′的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为测量平地上一块不规则区域(图中的阴影部分)的面积,画一个边长为2cm的正方形,使不规则区域落在正方形内,现向正方形内随机投掷小石子(假设小石子落在正方形内每一点都是等可能的),经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数0.25附近,由此可估计不规则区域的面积是m2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由于各人的习惯不同,双手交叉时左手大拇指在上或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如表所示:
2011届
2012届
2013届
2014届
2015届
参与实验的人数
106
110
98
104
112
右手大拇指在上的人数
54
57
49
51
56
频率
0.509
0.518
0.500
0.490
0.500
根据表格中的数据,你认为在这个随机事件中,右手大拇指在上的概率可以估计为 .

-
科目: 来源: 题型:
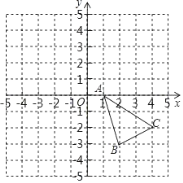
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(1,0),B(2,﹣3),C(4,﹣2).
(1)①画出△ABC关于x轴的对称图形△A1B1C1;②画出△A1B1C1向左平移3个单位长度后得到的△A2B2C2;
(2)如果AC上有一点P(m,n)经过上述两次变换,那么对应A2C2上的点P2的坐标.
相关试题

