搜索
【题目】在下列四个选项中，不适合普查的是
A. 了解全班同学每周体育锻炼的时间
B. 学校招聘新教师，对应聘教师面试
C. 鞋厂检查生产鞋底能承受的弯折次数
D. 安庆市某中学调查九年级全体540名学生数学成绩
参考答案：
【答案】C
【解析】
一般当调查的对象很多又不是每个数据都有很大的意义，或着调查的对象虽然不多，但是带有破坏性，应采用抽查方式；如果调查对象不需要花费太多的时间又不具有破坏性或者生产生活中有关安全隐患的问题就必须采用普查的调查方式进行，由于检查生产鞋底能承受的弯折次数有破坏性，所以不适合普查，故选C.
-
科目： 来源： 题型：
查看答案和解析>>【题目】若∠α的补角为60°，∠β的余角为60°,则∠α和∠β的大小关系是
A. ∠α＜∠β B. ∠α＞∠β C. ∠α=∠β D. 无法确定
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题提出
（1）如图①，已知△ABC，请画出△ABC关于直线AC对称的三角形．
问题探究
（2）如图②，在矩形ABCD中，AB=4，AD=6，AE=4，AF=2，是否在边BC、CD上分别存在点G、H，使得四边形EFGH的周长最小？若存在，求出它周长的最小值；若不存在，请说明理由．
问题解决
（3）如图③，有一矩形板材ABCD，AB=3米，AD=6米，现想从此板材中裁出一个面积尽可能大的四边形EFGH部件，使∠EFG=90°，EF=FG=
米，∠EHG=45°，经研究，只有当点E、F、G分别在边AD．AB、BC上，且AF＜BF，并满足点H在矩形ABCD内部或边上时，才有可能裁出符合要求的部件，试问能否裁得符合要求的面积尽可能大的四边形EFGH部件？若能，求出裁得的四边形EFGH部件的面积；若不能，请说明理由．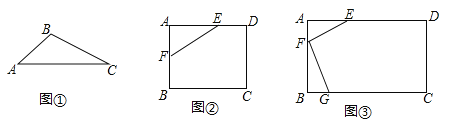
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题背景：
如图①，在四边形ADBC中，∠ACB=∠ADB=90°，AD=BD，探究线段AC，BC，CD之间的数量关系．
小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图②），易证点C，A，E在同一条直线上，并且△CDE是等腰直角三角形，所以CE=
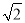CD，从而得出结论：AC+BC=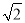CD．简单应用：
（1）在图①中，若AC=
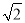，BC=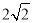
，则CD= ．（2）如图③，AB是⊙O的直径，点C、D在⊙上，
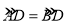，若AB=13，BC=12，求CD的长．拓展规律：
（3）如图④，∠ACB=∠ADB=90°，AD=BD，若AC=m，BC=n（m＜n），求CD的长（用含m，n的代数式表示）
（4）如图⑤，∠ACB=90°，AC=BC，点P为AB的中点，若点E满足AE=
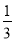AC，CE=CA，点Q为AE的中点，则线段PQ与AC的数量关系是 ．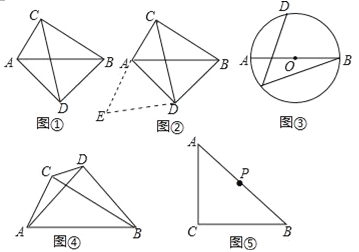
-
科目： 来源： 题型：
查看答案和解析>>【题目】2015年初，一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃，将300000用科学记数法表示为（ ）
A.3×106
B.3×105
C.0.3×106
D.30×104 -
科目： 来源： 题型：
查看答案和解析>>【题目】若+800元表示盈利800元，那么﹣300元表示（ ）
A. 收入300元 B. 盈利300元 C. 亏损300元 D. 支出300元
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面说法错误的是（ ）
A.两点确定一条直线
B.同角的补角相等
C.等角的余角相等
D.射线AB也可以写作射线BA
相关试题
