【题目】如图,在平面直角坐标系中, ![]() 是边长为
是边长为![]() 的等边三角形,直线
的等边三角形,直线![]() 与
与![]() 轴、
轴、![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() 、
、![]() .
. ![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
(![]() )点
)点![]() 的坐标为__________.(结果保留根号)
的坐标为__________.(结果保留根号)
(![]() )求证:点
)求证:点![]() 、
、![]() 关于
关于![]() 轴对称.
轴对称.
(![]() )若
)若![]() ,求直线
,求直线![]() 对应的函数表达式.
对应的函数表达式.

参考答案:
【答案】(![]() )
)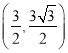 .(
.(![]() )证明见解析.(
)证明见解析.(![]() )
)![]()
【解析】试题分析:(1)过点A作AM⊥x轴于点M,根据等边三角形的性质可知:AO=3,∠AOM=60°,在Rt△AMO中利用30°角的对边为斜边的一半结合勾股定理可求出AM、OM的长,从而得出点A的坐标;
(2)由EF∥OA利用平行线的性质可得出∠BFE=∠BOA=60°,结合∠OBA=60°可得出△BEF为等边三角形,根据等边三角形的性质即可得出BE=BF可得出BE=BF、BO=BA,进而即可得出AE=OF,再由OC=AE即可得出OC=OF,从而证出点C、F关于y轴对称;
(3)设OC=OF=x,根据边与边的关系找出∠OCD=∠ODC,再根据平行线的性质即可得出∠CEF=∠CDO=∠ECF,进而可得出CF=EF,由此即可得出关于x的一元一次方程,解方程即可求出x的值,进而可得出点C、D的坐标,利用待定系数法即可求出直线l对应的函数表达式.
试题解析:解:(1)过点A作AM⊥x轴于点M,如图1所示.
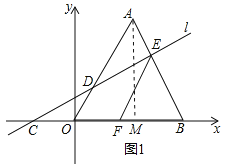
∵△A0B是边长为3的等边三角形,∴AB=OB=OA=3,且∠AOM=60°.
在Rt△AMO中,OA=3,∠AOM=60°,∴∠OAM=30°,∴OM=![]() OA=
OA=![]() ,AM=
,AM=![]() =
=![]() ,∴点A的坐标为(
,∴点A的坐标为(![]() ,
, ![]() ).
).
(2)证明:若证C、F关于y轴对称,只需证OC=OF即可.
∵EF∥OA,∴∠BFE=∠BOA=60°,∵∠OBA=60°,∴△BEF为等边三角形,∴BE=BF.
∵△AOB是等边三角形,∴BO=BA,∴AE=AB﹣BE=OB﹣BE=OF,又∵0C=AE,∴OC=OF,∴点C、F关于y轴对称.
(3)设OC=OF=x,∵OB=3,∴BF=EF=3﹣x,∵AD=EF,∴AD=3﹣x.
∵OA=3,∴OD=x,∴∠OCD=∠ODC.
∵OA∥EF,∴∠CEF=∠CDO=∠ECF,∴EF=CF,即3﹣x=2x,解得:x=1,∴点C的坐标为(﹣1,0),点D的坐标为(![]() ,
, ![]() ).
).
设直线l对应的函数表达式为y=kx+b,将点C(﹣1,0)、点D(![]() ,
, ![]() )代入直线l对应的函数表达式中,得
)代入直线l对应的函数表达式中,得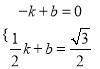 ,解得:
,解得: 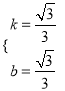 .
.
故直线l对应的函数表达式为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点
 ,
,  ,
,  .下列说法正确的是( )
.下列说法正确的是( )
A. △
 与△ABC是位似图形,位似中心是点(1,0)
与△ABC是位似图形,位似中心是点(1,0)B. △
 与△ABC是位似图形,位似中心是点(0,0)
与△ABC是位似图形,位似中心是点(0,0)C. △
 与△ABC是相似图形,但不是位似图形
与△ABC是相似图形,但不是位似图形D. △
 与△ABC不是相似图形
与△ABC不是相似图形 -
科目: 来源: 题型:
查看答案和解析>>【题目】有一个质地均匀的正12面体,12个面上分别写有1~12这12个整数(每个面只有一个整数且互不相同).投掷这个正12面体一次,记事件A为“向上一面的数字是2或3的整数倍”,记事件B为“向上一面的数字是3的整数倍”,请你判断等式P(A)=
 +P(B)是否成立,并说明理由.
+P(B)是否成立,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD和四边形
 位似,位似比
位似,位似比 =2,四边形A′B′C′D′和四边形
=2,四边形A′B′C′D′和四边形 位似,位似比
位似,位似比 =1.四边形
=1.四边形 和四边形ABCD是位似图形吗?位似比是多少?
和四边形ABCD是位似图形吗?位似比是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有“20”,“08”和“北京”的字块,如果婴儿能够排成“2008北京”或者“北京2008”.则他们就给婴儿奖励,假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为___________.

-
科目: 来源: 题型:
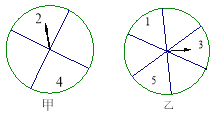
查看答案和解析>>【题目】你喜欢玩游戏吗?现请你玩一个转盘游戏.如图所示的两上转盘中指针落在每一个数字上的机会均等,现同时自由转动甲、乙两个转盘,转盘停止后,指针各指向一个数字,用所指的两个数字作乘积.所有可能得到的不同的积分别为_______________________;数字之积为奇数的概率为______.
相关试题

