【题目】如图,在长和宽分别是a,b的长方形的四个角都剪去一个边长为x的正方形,折叠后,做成一无盖的盒子(单位:cm).
(1)用a,b,x表示纸片剩余部分的面积;
(2)用a,b,x表示盒子的体积;
(3)当a=10,b=8且剪去的每一个小正方形的面积等于4 cm2时,求剪去的每一个正方形的边长及所做成的盒子的体积.

参考答案:
【答案】(1) (ab-4x2)cm2(2) x(a-2x)(b-2x)cm3(3) 48cm3
【解析】
(1)剩余部分的面积=原矩形的面积-四个小正方形的面积;
(2)体积=底面积×高;
(3)根据正方形的面积求x的值,代入(2)所得的代数式即可求得体积.
(1)剩余部分的面积(ab4x2)cm2;
(2)盒子的体积为:x(a2x)(b2x)cm3;
(3)由x2=4,得x=2,
当a=10,b=8,x=2时,
x(a2x)(b2x),
=2(102×2)(82×2),
=2×6×4,
=48(cm3).
答:盒子的体积为48立方厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.

(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数a、b,定义一种运算“
 ”为:ab=a2 +ab-2,有下列命题:
”为:ab=a2 +ab-2,有下列命题:①1
 3=2;
3=2; ②方程x
 1=0的根为:x1 =-2,x2 =1;
1=0的根为:x1 =-2,x2 =1; ③不等式组
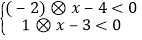 的解集为:-1<x<4;
的解集为:-1<x<4; ④点(
 ,
,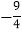 )在函数y=x
)在函数y=x (-1)的图象上.
(-1)的图象上. 其中正确的是( )
A. ①②③④ B. ①③ C. ①②③ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将-2,-1,0,1,2,3,4,5,6,7这10个数分别填写在五角星中每两条线的交点处(每个交点处只填写一个数),将每一条线上的4个数相加,共得5个数,设为a1,a2,a3,a4,a5.
(1)求
 (a1+a2+a3+a4+a5)的值;
(a1+a2+a3+a4+a5)的值;(2)交换其中任何两位数的位置后,
 (a1+a2+a3+a4+a5)的值是否改变?并说明理由.
(a1+a2+a3+a4+a5)的值是否改变?并说明理由.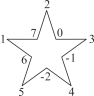
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作圆的切线.
已知:P为⊙O外一点.
求作:经过点P的⊙O的切线.
小敏的作法如下:
如图,
(1)连接OP,作线段OP的垂直平分线MN交OP于点C;
(2)以点C为圆心,CO的长为半径作圆,交⊙O于A,B两点;
(3)作直线PA,PB.所以直线PA,PB就是所求作的切线.
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是 ;由此可证明直线PA,PB都是⊙O的切线,其依据是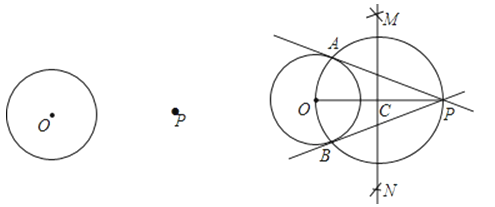
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=12,BC=15,AD⊥BC于点D,∠BAD=30°,求tanC的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是最大的负整数,b是多项式2m2n-m3n2-m-2的次数,c是单项式-2xy2的系数,且a,b,c分别是点A,B,C在数轴上对应的数.
(1)求a,b,c的值,并在数轴上标出点A,B,C;

(2)若动点P,Q同时从A,B出发沿数轴负方向运动,点P的速度是每秒
 个单位长度,点Q的速度是每秒2个单位长度,求运动几秒后,点Q可以追上点P?
个单位长度,点Q的速度是每秒2个单位长度,求运动几秒后,点Q可以追上点P?(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于10,请直接写出所有点M对应的数.(不必说明理由)
相关试题

