【题目】如图,已知点A(0,4),B(8,0),C(8,4),连接AC,BC得到四边形AOBC,点D在边AC上,连接OD,将边OA沿OD折叠,点A的对应点为点P,若点P到四边形AOBC较长两边的距离之比为1:3,则点P的坐标为__________________.

参考答案:
【答案】(![]() ,3)或(
,3)或(![]() ,1)或(2
,1)或(2![]() ,﹣2).
,﹣2).
【解析】
由已知得出∠A=90°,BC=OA=4,OB=AC=8,分两种情况:
(1)当点P在矩形AOBC的内部时,过P作OB的垂线交OB于F,交AC于E,当PE:PF=1:3时,求出PE=1,PF=3,由折叠的性质得:OP=OA=4,∠OPD=∠A=90°.在Rt△OPF中,由勾股定理求出OF的长,即可得出答案;
②当PE:PF=3:1时,同理得P的坐标;
(2)当点P在矩形AOBC的外部时,此时点P在第四象限,过P作OB的垂线交OB于F,交AC于E,由PF:PE=1:3,则PF:EF=1:2,求出PF=2.在Rt△OPF中,由勾股定理求出OF的长,即可得出答案.
∵点A(0,4),B(8,0),C(8,4),∴BC=OA=4,OB=AC=8,分两种情况:
(1)当点P在矩形AOBC的内部时,过P作OB的垂线交OB于F,交AC于E,如图1所示.
①当PE:PF=1:3时.
∵PE+PF=BC=4,∴PE=1,PF=3,由折叠的性质得:OP=OA=4.在Rt△OPF中,由勾股定理得:OF=![]() =
=![]() =
=![]() ,∴P(
,∴P(![]() ,3);
,3);
②当PE:PF=3:1时,同理得:P(![]() ,1);
,1);
(2)当点P在矩形AOBC的外部时,此时点P在第四象限,过P作OB的垂线交OB于F,交AC于E,如图2所示.
∵PF:PE=1:3,则PF:EF=1:2,∴PF=![]() EF=
EF=![]() BC=2,由折叠的性质得:OP=OA=4.在Rt△OA'F中,由勾股定理得:OF=
BC=2,由折叠的性质得:OP=OA=4.在Rt△OA'F中,由勾股定理得:OF=![]() =2
=2![]() ,∴P(2
,∴P(2![]() ,﹣2);
,﹣2);
综上所述:点P的坐标为(![]() ,3)或(
,3)或(![]() ,1)或(2
,1)或(2![]() ,﹣2).
,﹣2).
故答案为:(![]() ,3)或(
,3)或(![]() ,1)或(2
,1)或(2![]() ,﹣2).
,﹣2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+2
 x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+
x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+ AP的最小值为( )
AP的最小值为( )
A.
 B.
B. 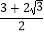 C. 3 D. 2
C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:对于两个不等的非零实数
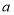 、
、 ,若分式
,若分式 的值为零,则
的值为零,则 或
或 .又因为
.又因为 ,所以关于
,所以关于 的方程
的方程 有两个解,分别为
有两个解,分别为 ,
, .
.应用上面的结论解答下列问题:
(1)方程
 的两个解分别为
的两个解分别为 ,
, ,则
,则 _________,
_________, _________;
_________;(2)方程
 的两个解分别为
的两个解分别为 ,
, ,求
,求 的值;
的值;(3)关于
 的方程
的方程 的两个解分别为
的两个解分别为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
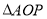 为等边三角形,
为等边三角形, 点坐标为
点坐标为 ,点
,点 为
为 轴上位于
轴上位于 点上方的一个动点,以
点上方的一个动点,以 为边向
为边向 的右侧作等边
的右侧作等边 ,连接
,连接 ,并延长
,并延长 交
交 轴于点
轴于点 .
.
(1)求证:
 ;
;(2)当点
 在运动时,
在运动时, 是否平分
是否平分 ?请说明理由;
?请说明理由;(3)当点
 在运动时,在
在运动时,在 轴上是否存在点
轴上是否存在点 ,使得
,使得 为等腰三角形?若存在,请求出点
为等腰三角形?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 中,对角线
中,对角线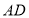 平分
平分 ,
, ,
, ,则
,则 的度数为( )
的度数为( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 的平分线与
的平分线与 的垂直平分线相交于点
的垂直平分线相交于点 ,
, ,
, ,垂足分别为
,垂足分别为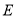 、
、 ,
, ,
, ,则
,则 的长为______.
的长为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船以每小时40海里的速度在海面上航行,当该轮船行驶到B处时,发现灯塔C在它的东北方向,轮船继续向北航行,30分钟后到达A处,此时发现灯塔C在它的北偏东75°方向上,求此时轮船与灯塔C的距离.(结果保留根号)

相关试题

