搜索
【题目】用简便方法计算：
（1）20192﹣2018×2020
（2）820×0.12521．
参考答案：
【答案】（1）1；（2）0.125
【解析】
(1)将2018×2020变形为(2019-1)×(2019+1)，再利用平方差公式展开、计算可得；
(2)原式变形为820×0.12520×0.125，再利用积的乘方的运算法则计算可得．
(1)20192﹣2018×2020
=20192﹣(2019﹣1)×(2019+1)
=20192﹣20192+1
=1；
(2)820×0.12521
=820×0.12520×0.125
=(8×0.125)20×0.125
=120×0.125
=1×0.125
=0.125．
-
科目： 来源： 题型：
查看答案和解析>>【题目】5月16日，我校进行了全校师生防灾减灾大演练，警报拉响后同学们匀速跑步到操场，在操场指定位置清点人数、听广播后，再沿原路匀速步行回教室，同学们离开教学楼的距离y与时间x的关系的大致图象是（ ）
A.
B. 
C. 
D.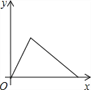 
-
科目： 来源： 题型：
查看答案和解析>>【题目】同学们，我们曾经研究过n×n的正方形网格，得到了网格中正方形的总数的表达式为12+22+32+…+n2 ． 但n为100时，应如何计算正方形的具体个数呢？下面我们就一起来探究并解决这个问题．首先，通过探究我们已经知道0×1+1×2+2×3+…+（n﹣l）×n
=
n（n+1）（n﹣1）时，我们可以这样做：
（1）观察并猜想：
12+22=（1+0）×1+（1+1）×2=l+0×1+2+1×2=（1+2）+（0×1+1×2）
12+22+32=（1+0）×1+（1+1）×2+（l+2）×3
=1+0×1+2+1×2+3+2×3
=（1+2+3）+（0×1+1×2+2×3）
12+22+32+42=（1+0）×1+（1+1）×2+（l+2）×3+
=1+0×1+2+1×2+3+2×3+
=（1+2+3+4）+（）
…
（2）归纳结论：
12+22+32+…+n2=（1+0）×1+（1+1）×2+（1+2）×3+…[1+（n﹣l）]n
=1+0×1+2+1×2+3+2×3+…+n+（n﹣1）×n
=（）+[]
=+
=
×
（3）实践应用：
通过以上探究过程，我们就可以算出当n为100时，正方形网格中正方形的总个数是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在△ABC中，∠ACB＝90°点E是AB的中点，连接CE，过点E作ED⊥BC于点D，在DE的延长线上取一点F，使AF＝CE，求证四边形ACEF是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于不等式组
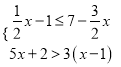下列说法正确的是（ ）A. 此不等式组无解 B. 此不等式组有7个整数解
C. 此不等式组的负整数解是﹣3，﹣2，﹣1 D. 此不等式组的解集是
＜x≤2 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ACB中，∠C=90°，BE平分∠ABC，ED垂直平分AB于D，则图中的全等三角形对数共有（ ）
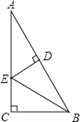
A. 1对 B. 2对 C. 3对 D. 4对
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y＝－2x与直线y＝kx＋b相交于点A(a,2)，并且直线y＝kx＋b经过x轴上点B(2,0)．
(1)求直线y＝kx＋b的解析式；
(2)求两条直线与y轴围成的三角形面积；
(3)直接写出不等式(k＋2)x＋b≥0的解集．
相关试题
