【题目】如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )
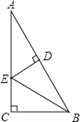
A. 1对 B. 2对 C. 3对 D. 4对
参考答案:
【答案】C
【解析】分析:由在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB,利用HL易证得Rt△EBC≌Rt△EBD与Rt△EAD≌Rt△EBD,继而可得△AED≌△BCE.
详解:∵ED垂直平分AB,
∴AE=BE,ED⊥AB,
∵在Rt△ACB中,∠C=90°,BE平分∠ABC,
∴EC=ED,
在Rt△ECB和Rt△EDB中,
EC=ED,BE=BE,
∴Rt△EBC≌Rt△EBD(HL),
在Rt△EAD和Rt△EBD中,
AE=BE,DE=DE,
∴Rt△EAD≌Rt△EBD(HL),
∴△AED≌△BCE.
∴图中的全等三角形对数共有3对.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠ACB=90°点E是AB的中点,连接CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE,求证四边形ACEF是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用简便方法计算:
(1)20192﹣2018×2020
(2)820×0.12521.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于不等式组
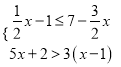 下列说法正确的是( )
下列说法正确的是( )A. 此不等式组无解 B. 此不等式组有7个整数解
C. 此不等式组的负整数解是﹣3,﹣2,﹣1 D. 此不等式组的解集是
 <x≤2
<x≤2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=-2x与直线y=kx+b相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0).
(1)求直线y=kx+b的解析式;
(2)求两条直线与y轴围成的三角形面积;
(3)直接写出不等式(k+2)x+b≥0的解集.

-
科目: 来源: 题型:
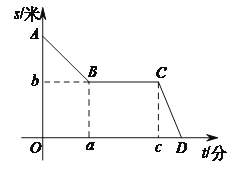
查看答案和解析>>【题目】李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程为2000米.一天,李老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.李老师回家过程中,离家的路程s(米)与所用时间t(分)之间的关系如图所示.
(1)求a,b,c的值;
(2)求李老师从学校到家的总时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑经销商计划同时购进一批电脑机箱和液晶显示器,若购进电脑机箱10台,和液晶显示器8台,共需要资金7000元,若购进电脑机箱两台和液晶显示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商计划购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元,根据市场行情,销售电脑机箱,液晶显示器一台分别可获得10元和160元,改经销商希望销售完这两种商品,所获得利润不少于4100元,试问:该经销商有几种进货方案?哪种方案获利最大?最大利润是多少?
相关试题

