【题目】如图,将矩形OABC放在平面直角坐标系中,O为原点,点A在x轴的正半轴上,B(8,6),点D是射线AO上的一点,把△BAD沿直线BD折叠,点A的对应点为A′.
(Ⅰ)若点A′落在矩形的对角线OB上时,OA′的长= ;
(Ⅱ)若点A′落在边AB的垂直平分线上时,求点D的坐标;
(Ⅲ)若点A′落在边AO的垂直平分线上时,求点D的坐标(直接写出结果即可).

参考答案:
【答案】(Ⅰ)6;(Ⅱ)D(8﹣2![]() ,0);(Ⅲ)点D的坐标为(3
,0);(Ⅲ)点D的坐标为(3![]() ﹣1,0)或(﹣3
﹣1,0)或(﹣3![]() ﹣1,0).
﹣1,0).
【解析】分析:(Ⅰ)由点B的坐标知OA=8、AB=6、OB=10,根据折叠性质可得BA=BA′=6,据此可得答案;
(Ⅱ)连接AA′,利用折叠的性质和中垂线的性质证△BAA′是等边三角形,可得∠A′BD=∠ABD=30°,据此知AD=ABtan∠ABD=2![]() ,继而可得答案;
,继而可得答案;
(Ⅲ)分点D在OA上和点D在AO延长线上这两种情况,利用相似三角形的判定和性质分别求解可得.
详解:(Ⅰ)如图1,由题意知OA=8、AB=6,∴OB=10,由折叠知,BA=BA′=6,∴OA′=6.
故答案为:6;

(Ⅱ)如图2,连接AA′.
∵点A′落在线段AB的中垂线上,∴BA=AA′.
∵△BDA′是由△BDA折叠得到的,
∴△BDA′≌△BDA,∴∠A′BD=∠ABD,A′B=AB,
∴AB=A′B=AA′,∴△BAA′是等边三角形,
∴∠A′BA=60°,∴∠A′BD=∠ABD=30°,
∴AD=ABtan∠ABD=6tan30°=2![]() ,
,
∴OD=OA﹣AD=8﹣2![]() ,
,
∴点D(8﹣2![]() ,0);
,0);

(Ⅲ)①如图3,当点D在OA上时.
由旋转知△BDA′≌△BDA,∴BA=BA′=6,∠BAD=∠BA′D=90°.
∵点A′在线段OA的中垂线上,∴BM=AN=![]() OA=4,∴A′M=
OA=4,∴A′M=![]() =
=![]() =2
=2![]() ,
,
∴A′N=MN﹣A′M=AB﹣A′M=6﹣2![]() ,
,
由∠BMA′=∠A′ND=∠BA′D=90°知△BMA′∽△A′ND,
则![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:DN=3![]() ﹣5,
﹣5,
则OD=ON+DN=4+3![]() ﹣5=3
﹣5=3![]() ﹣1,
﹣1,
∴D(3![]() ﹣1,0);
﹣1,0);

②如图4,当点D在AO延长线上时,过点A′作x轴的平行线交y轴于点M,延长AB交所作直线于点N, 则BN=CM,MN=BC=OA=8,由旋转知△BDA′≌△BDA,∴BA=BA′=6,∠BAD=∠BA′D=90°.
∵点A′在线段OA的中垂线上,∴A′M=A′N=![]() MN=4,
MN=4,
则MC=BN=![]() =2
=2![]() ,∴MO=MC+OC=2
,∴MO=MC+OC=2![]() +6,
+6,
由∠EMA′=∠A′NB=∠BA′D=90°知△EMA′∽△A′NB,
则![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:ME=![]() ,则OE=MO﹣ME=6+
,则OE=MO﹣ME=6+![]() .
.
∵∠DOE=∠A′ME=90°、∠OED=∠MEA′,
∴△DOE∽△A′ME,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:DO=3![]() +1,则点D的坐标为(﹣3
+1,则点D的坐标为(﹣3![]() ﹣1,0).
﹣1,0).
综上,点D的坐标为(3![]() ﹣1,0)或(﹣3
﹣1,0)或(﹣3![]() ﹣1,0).
﹣1,0).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在抗洪抢险救灾中,某地粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到没有受洪水威胁的A,B两仓库,已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为60吨,B库的容量为120吨,从甲、乙两库到A、B两库的路程和运费如表(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米)
运费(元/吨千米)
甲库
乙库
甲库
乙库
A库
20
15
12
12
B库
25
20
10
8
若从甲库运往A库粮食x吨,
(Ⅰ)填空(用含x的代数式表示):
①从甲库运往B库粮食 吨;
②从乙库运往A库粮食 吨;
③从乙库运往B库粮食 吨;
(Ⅱ)写出将甲、乙两库粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式,并求出当从甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工人计划加工一批产品,如果每小时加工产品10个,就可以在预定时间完成任务,如果每小时多加工2个,就可以提前1小时完成任务.
(1)该产品的预定加工时间为几小时?
(2)若该产品销售时的标价为100元/个,按标价的八折销售时,每个仍可以盈利25元,该批产品总成本为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后,分别位于点Q、R处,且相距30海里,如果知道“远航”号沿北偏东
 方向航行,请求出“海天”号的航行方向?
方向航行,请求出“海天”号的航行方向?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
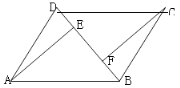
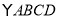 中,BD是它的一条对角线,过A、C两点分别作
中,BD是它的一条对角线,过A、C两点分别作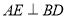 ,
,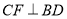 ,E、F为垂足.
,E、F为垂足.(1)如图,求证:
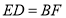 ;
;
(2)如图,连接AC,设AC、BD交于点O,若
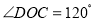 .在不添加任何辅助线的情况下,请直接写出图中的所有长度是OE长度2倍的线段.
.在不添加任何辅助线的情况下,请直接写出图中的所有长度是OE长度2倍的线段.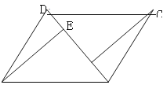
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2﹣6x+9与直线y=x+3交于A,B两点(点A在点B的左侧),抛物线的顶点为C,直线y=x+3与x轴交于点D.
(Ⅰ)求抛物线的顶点C的坐标及A,B两点的坐标;
(Ⅱ)将抛物线y=x2﹣6x+9向上平移1个单位长度,再向左平移t(t>0)个单位长度得到新抛物线,若新抛物线的顶点E在△DAC内,求t的取值范围;
(Ⅲ)点P(m,n)(﹣3<m<1)是抛物线y=x2﹣6x+9上一点,当△PAB的面积是△ABC面积的2倍时,求m,n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地2016年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2018年在2016年的基础上增加投入资金1600万元.
(1)从2016年到2018年,该地投入异地安置资金的年平均增长率为多少?
(2)在2018年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前800户(含第800户)每户每天奖励10元,800户以后每户每天奖励5元,按租房400天计算,求2018年该地至少有多少户享受到优先搬迁租房奖励.
相关试题

