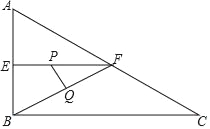
【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=2cm,E、F分别是AB、AC的中点,动点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时动点Q从点B出发,沿BF方向匀速运动,速度为2cm/s,连接PQ,设运动时间为ts(0<t<1),则当t=___时,△PQF为等腰三角形.
参考答案:
【答案】2﹣![]() 或
或![]() .
.
【解析】
由勾股定理和含30°角的直角三角形的性质先分别求出AC和BC,然后根据题意把PF和FQ表示出来,当△PQF为等腰三角形时分三种情况讨论即可.
解:∵∠ABC=90°,∠ACB=30°,AB=2cm,
∴AC=2AB=4cm,BC=![]() =2
=2![]() ,
,
∵E、F分别是AB、AC的中点,
∴EF=![]() BC=
BC=![]() cm,BF=
cm,BF=![]() AC=2cm,
AC=2cm,
由题意得:EP=t,BQ=2t,
∴PF=![]() ﹣t,FQ=2﹣2t,
﹣t,FQ=2﹣2t,
分三种情况:
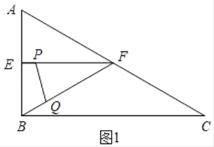
①当PF=FQ时,如图1,△PQF为等腰三角形.
则![]() ﹣t=2﹣2t,
﹣t=2﹣2t,
t=2﹣![]() ;
;
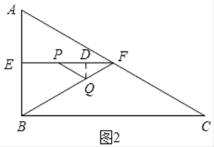
②如图2,当PQ=FQ时,△PQF为等腰三角形,过Q作QD⊥EF于D,
∴PF=2DF,
∵BF=CF,
∴∠FBC=∠C=30°,
∵E、F分别是AB、AC的中点,
∴EF∥BC,
∴∠PFQ=∠FBC=30°,
∵FQ=2﹣2t,
∴DQ=![]() FQ=1﹣t,
FQ=1﹣t,
∴DF= ![]() (1﹣t),
(1﹣t),
∴PF=2DF=2![]() (1﹣t),
(1﹣t),
∵EF=EP+PF= ![]() ,
,
∴t+2![]() (1﹣t)=
(1﹣t)=![]() ,
,
t= ![]() ;
;
③因为当PF=PQ时,∠PFQ=∠PQF=30°,
∴∠FPQ=120°,
而在P、Q运动过程中,∠FPQ最大为90°,所以此种情况不成立;
综上,当t=2﹣![]() 或
或![]() 时,△PQF为等腰三角形.
时,△PQF为等腰三角形.
故答案为:2﹣![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将直角三角形ABC沿着BC方向平移
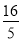 cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么图中阴影部分的面积为____ cm 2.
cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么图中阴影部分的面积为____ cm 2.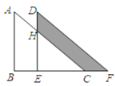
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
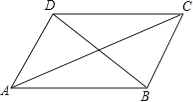
A.①②B.②③C.①③D.②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依此为2,4,6,8,...,顶点依此用A1,A2,A3,A4......表示,则顶点A55的坐标是___.
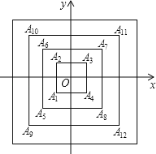
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校开展的“书香校园”活动受到同学们的广泛关注,为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计图表.
学生借阅图书的次数统计表:
借阅图书的次数
 次
次 次
次 次
次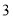 次
次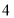 次及以上
次及以上人数

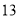
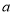

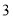

请你根据统计图表中的信息,解答下列问题:
(1)
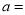 ,
,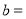 ;
;(2)该调查统计数据的中位数是 ,众数是 ;
(3)若该校共有
 名学生,根据调查结果,估计该校学生在一周内借阅图书
名学生,根据调查结果,估计该校学生在一周内借阅图书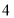 次及以上的人数.
次及以上的人数. -
科目: 来源: 题型:
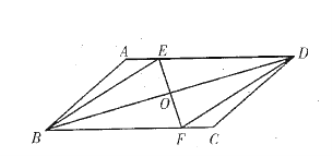
查看答案和解析>>【题目】如图,已知平行四边形
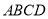 中,
中,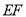 垂直平分线段
垂直平分线段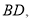 连接
连接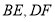
(1)求证:四边形
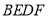 是菱形;
是菱形;(2)若
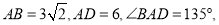 求
求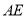 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取
 =1.732,结果精确到1m)
=1.732,结果精确到1m)
相关试题

