搜索
【题目】如图，直线AE、CF分别被直线EF、AC所截，已知，∠1=∠2，AB平分∠EAC，CD平分∠ACG．将下列证明AB∥CD的过程及理由填写完整．
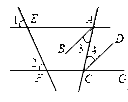
证明：∵ ∠1="∠2" （ 已知 ）
∴ AE∥ （ ）
∴ ∠EAC =∠ ，（ ）
而AB平分∠EAC，CD平分∠ACG（ 已知 ）
∴∠ =
∠EAC，∠4=∠ （ 角平分线的定义 ）
∴∠ =∠4（等量代换）
∴AB∥CD（ ）．
参考答案：
【答案】见解析
【解析】
根据平行线的判定和性质进行填空即可．
∵∠1="∠2" （已知）
∴AE∥ PG （同位角相等，两直线平行 ）
∴∠EAC =∠ ACG ，（ 两直线平行，内错角相等 ）
而 AB平分∠EAC，CD平分∠ACG（ 已知 ）
∴∠ 3 =
∠EAC，∠4=∠ ACG （ 角平分线的定义 ）
∴∠ 3 =∠4（等量代换）
∴B∥CD（ 内错角相等，两直线平行）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂为了解甲、乙两个部门员工的生产技能情况，从甲、乙两个部门各随机抽取20名员工，进行生产技能测试，测试成绩（百分制）如下：
甲7886 748175768770759075798170748086698377
乙9373 888172819483778380817081737882807040
（说明：成绩80分及以上为优秀，70-79分为良好，60-69分为合格，60分以下为不合格）
（1）请填完整表格：
部门
平均数
中位数
众数
甲
78.3
75
乙
78
80.5
（2）从样本数据可以推断出 部门员工的生产技能水平较高，请说明理由．（至少从两个不同的角度说明推断的合理性）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，正方形纸片ABCD的边长为2，翻折∠B、∠D，使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕（如图2）．设AE＝x（0＜x＜2），给出下列判断：①当x=1时，点P是正方形ABCD的中心；②当x＝
时，EF+GH＞AC；③当0＜x＜2时，六边形AEFCHG面积的最大值是3；④当0＜x＜2时，六边形AEFCHG周长的值不变．其中正确的选项是（ ）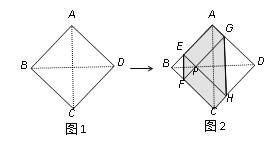
A. ①③ B. ①②④ C. ①③④ D. ①②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】福建省教育厅日前发布文件，从2019年开始，体育成绩将按一定的原始分计入中考总分。某校为适应新的中考要求，决定为体育组添置一批体育器材。学校准备在网上订购一批某品牌足球和跳绳，在查阅天猫网店后发现足球每个定价150元，跳绳每条定价30元．现有A、B两家网店均提供包邮服务，并提出了各自的优惠方案．
A网店：买一个足球送一条跳绳；
B网店：足球和跳绳都按定价的90%付款．
已知要购买足球40个，跳绳x条（x＞40）
（1）若在A网店购买，需付款 元（用含x的代数式表示）.
若在B网店购买，需付款 元（用含x的代数式表示）.
（2）若x=100时，通过计算说明此时在哪家网店购买较为合算？
（3）当x=100时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法，
并计算需付款多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知数轴上点A表示的数为﹣7，点B表示的数为5，点C到点A，点B的距离相等，动点P从点A出发，以每秒2个单位长度的速度沿数轴向右匀速运动，设运动的时间为t（t＞0）秒．
（1）点C表示的数是 ；
（2）求当t等于多少秒时，点P到达点B处；
（3）点P表示的数是 （用含有t的代数式表示）；
（4）求当t等于多少秒时，PC之间的距离为2个单位长度．
-
科目： 来源： 题型：
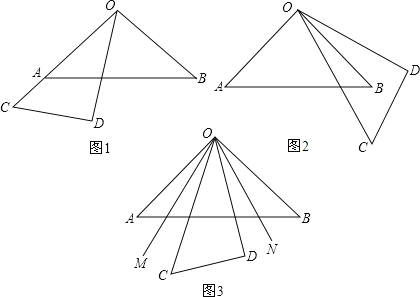
查看答案和解析>>【题目】已知将一副三角板（直角三角板OAB和直角三角板OCD，∠AOB＝90°，∠COD＝30°）如图1摆放，点O、A、C在一条直线上．将直角三角板OCD绕点O逆时针方向转动，变化摆放如图位置
（1）如图1，当点O、A、C在同一条直线上时，则∠BOD的度数是多少？
（2）如图2，若要OB恰好平分∠COD，则∠AOC的度数是多少？
（3）如图3，当三角板OCD摆放在∠AOB内部时，作射线OM平分∠AOC，射线ON平分∠BOD，如果三角板OCD在∠AOB内绕点O任意转动，∠MON的度数是否发生变化？如果不变，求其值；如果变化，说明理由．
-
科目： 来源： 题型：
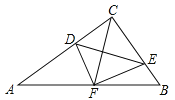
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，点D，E分别在AC，BC上，且∠CDE=∠B，将△CDE沿DE折叠，点C恰好落在AB边上的点F处．若AC=8，AB=10，则CD的长为 ．
相关试题
