【题目】如图,已知数轴上点A表示的数为﹣7,点B表示的数为5,点C到点A,点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(t>0)秒.
(1)点C表示的数是 ;
(2)求当t等于多少秒时,点P到达点B处;
(3)点P表示的数是 (用含有t的代数式表示);
(4)求当t等于多少秒时,PC之间的距离为2个单位长度.
![]()
参考答案:
【答案】(1) -1;(2)6;(3)﹣7+2t;(4)t=2 或t=4.
【解析】
(1)根据线段中点坐标公式可求点C表示的数;
(2)根据时间=路程÷速度,可求t的值;
(3)根据两点之间的距离公式可求点P表示的数;
(4)分P在点C左边和点C右边两种情况讨论求解.
(1)(﹣7+5)÷2=﹣2÷2=﹣1.
故点C表示的数是﹣1.
故答案为:﹣1;
(2)![]() =6;
=6;
(3)﹣7+2t;
故答案为:﹣7+2t;
(4)因为PC之间的距离为2个单位长度,所以点P运动到﹣3或1,即﹣7+2t=﹣3或﹣7+2t=1,
即t=2 或t=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G.点F是CD上一点,且满足
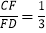 ,连接AF并延长交⊙O于点E.连接AD、DE,若CF=2,AF=3.给出下列结论:
,连接AF并延长交⊙O于点E.连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=
 ;④S△DEF=4
;④S△DEF=4 .
.其中正确的是( )
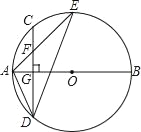
A. ①②④ B. ①②③ C. ②③④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲口袋中装有两个相同的小球,它们的标号分别为2和7,乙口袋中装有两个相同的小球,它们的标号分别为4和5,丙口袋中装有三个相同的小球,它们的标号分别为3,8,9.从这3个口袋中各随机地取出1个小球.
(1)求取出的3个小球的标号全是奇数的概率是多少?
(2)以取出的三个小球的标号分别表示三条线段的长度,求这些线段能构成三角形的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m长的影子如图所示,已知窗框的影子DE的点E到窗下墙脚的距离CE=3.9 m,窗口底边离地面的距离BC=1.2 m,试求窗口的高度(即AB的值).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.
(1)如图1,若AC:AB=1:2,EF⊥CB,求证:EF=CD;
(2)如图2,若AC:AB=1:
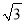 ,EF⊥CE,求EF: EG的值.
,EF⊥CE,求EF: EG的值.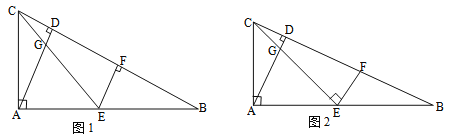
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)将下列各数填在相应的集合里.
﹣(﹣2.5),(﹣1)2,﹣|﹣2|,﹣22,0,
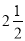 ,﹣1.5;
,﹣1.5;正数集合{ …}
分数集合{ …}
(2)把表示上面各数的点画在数轴上,再按从小到大的顺序,用“<“号把这些数连接起来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
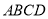 ,点
,点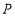 为对角线
为对角线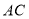 上一个动点,
上一个动点,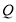 为
为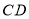 边上一点,且
边上一点,且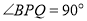 .
.(1)求证:
 ;
;(2)若四边形
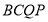 的面积为25,试探求
的面积为25,试探求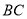 与
与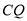 满足的数量关系式;
满足的数量关系式;(3)若
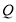 为射线
为射线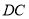 上的点,设
上的点,设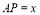 ,四边形
,四边形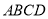 的周长为
的周长为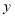 ,且
,且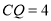 ,求
,求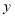 与
与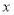 的函数关系式.
的函数关系式.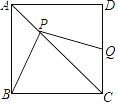
相关试题

