【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)试证明:无论![]() 取何值此方程总有两个实数根;
取何值此方程总有两个实数根;
(2)若原方程的两根![]() ,
,![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析;(2)-2.
【解析】(1)将原方程变形为一般式,根据方程的系数结合根的判别式,即可得出△=(2p+1)2≥0,由此即可证出:无论p取何值此方程总有两个实数根;
(2)根据根与系数的关系可得出x1+x2=5、x1x2=6-p2-p,结合x12+x22-x1x2=3p2+1,即可求出p值.
(1)证明:原方程可变形为x2-5x+6-p2-p=0.
∵△=(-5)2-4(6-p2-p)=25-24+4p2+4p=4p2+4p+1=(2p+1)2≥0,
∴无论p取何值此方程总有两个实数根;
(2)∵原方程的两根为x1、x2,
∴x1+x2=5,x1x2=6-p2-p.
又∵x12+x22-x1x2=3p2+1,
∴(x1+x2)2-3x1x2=3p2+1,
∴52-3(6-p2-p)=3p2+1,
∴25-18+3p2+3p=3p2+1,
∴3p=-6,
∴p=-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市在城市建设中,要折除旧烟囱AB(如图所示),在烟囱正西方向的楼CD的顶端C,测得烟囱的顶端A的仰角为45°,底端B的俯角为30°,已量得DB=21m.
(1)在原图上画出点C望点A的仰角和点C望点B的俯角,并分别标出仰角和俯角的大小;
(2)拆除时若让烟囱向正东倒下,试问:距离烟囱正东35m远的一棵大树是否被歪倒的烟囱砸着?请说明理由.(
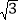 ≈1.732)
≈1.732)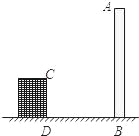
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别
时间(小时)
频数(人数)
频率
A
0≤t≤0.5
6
0.15
B
0.5≤t≤1
a
0.3
C
1≤t≤1.5
10
0.25
D
1.5≤t≤2
8
b
E
2≤t≤2.5
4
0.1
合计
1
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x
﹣1
0
1
3
y
﹣1
3
5
3
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.

(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】进入冬季,我市空气质量下降,多次出现雾霾天气.商场根据市民健康需要,代理销售一种防尘口罩,进货价为20元/包,经市场销售发现:销售单价为30元/包时,每周可售出200包,每涨价1元,就少售出5包.若供货厂家规定市场价不得低于30元/包,且商场每周完成不少于150包的销售任务.
(1)试确定周销售量y(包)与售价x(元/包)之间的函数关系式;
(2)试确定商场每周销售这种防尘口罩所获得的利润w(元)与售价x(元/包)之间的函数关系式,并直接写出售价x的范围;
(3)当售价x(元/包)定为多少元时,商场每周销售这种防尘口罩所获得的利润w(元)最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知 AB 是⊙O 的直径,点 C、D 在⊙O 上,过 D 点作 PF∥AC交⊙O 于 F,交 AB 于点 E,∠BPF=∠ADC
(1)求证:AEEB=DEEF.
(2)求证:BP 是⊙O 的切线:
(3)当的半径为
 ,AC=2,BE=1 时,求 BP 的长,
,AC=2,BE=1 时,求 BP 的长,
相关试题

