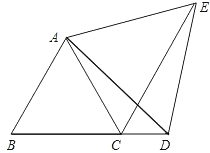
【题目】如图,等边△ABC中,点D在延长线上,CE平分∠ACD,且CE=BD.说明:△ADE是等边三角形.
参考答案:
【答案】详见解析.
【解析】试题分析:
要证△ADE为等边三角形,可以先证它为等腰三角形,再证该等腰三角形的一个内角为60°. 综合分析已知条件可知,可以利用△ABD和△ACE全等证明AD=AE. 根据已知条件和等边三角形的性质,不难证明∠B=∠ACE,进而利用SAS证明△ABD和△ACE全等. 利用全等三角形的性质可以得到△ADE是等腰三角形. 利用全等三角形的性质,通过相关角之间的和差关系,不难证明∠DAE=∠BAC=60°,从而证明△ADE为等边三角形.
试题解析:
证明:∵△ABC为等边三角形,
∴∠B=∠ACB=∠BAC=60°,AB=AC.
∵∠ACB=60°,
∴∠ACD=180°-∠ACB=180°-60°=120°,
∵CE平分∠ACD,
∴![]() .
.
∴∠B=∠ACE.
∵在△ABD和△ACE中,
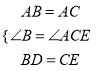 ,
,
∴△ABD≌△ACE (SAS),
∴AD=AE,∠BAD=∠CAE.
∵∠BAD=∠CAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAC=∠DAE=60°.
∵∠DAE=60°,AD=AE,
∴△ADE为等边三角形.
-
科目: 来源: 题型:
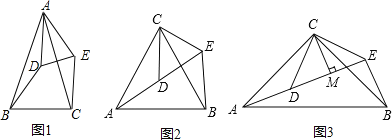
查看答案和解析>>【题目】(1)如图1,△ABC与△ADE均是顶角为40°的等腰三角形,BC、DE分别是底边,求证:BD=CE;
(2)如图2,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
填空:∠AEB的度数为 ;线段BE与AD之间的数量关系是 .
(3)拓展探究
如图3,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有( )
①同位角相等;
②若∠A+∠B+∠C=180°,则∠A、∠B、∠C互补;
③同一平面内的三条直线a、b、c,若a∥b,c与a相交,则c与b相交;
④同一平面内两条直线的位置关系可能是平行或垂直;
⑤有公共顶点并且相等的角是对顶角.
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥EF,∠BCD=135°,∠FDC=85°,则∠B+∠F的度数为( )

A.38°
B.40°
C.55°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的内角和是540°,则这个多边形是边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(﹣3,b)在第三象限内,则b( )
A. 是正数 B. 是负数
C. 是0 D. 可以是正数,也可以是负数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点A(2,﹣3)和点B关于原点对称,则点B的坐标为( )
A. (﹣2,3) B. (﹣2,﹣3) C. (2,﹣3) D. (2,3)
相关试题

