【题目】下列说法正确的有( )
①同位角相等;
②若∠A+∠B+∠C=180°,则∠A、∠B、∠C互补;
③同一平面内的三条直线a、b、c,若a∥b,c与a相交,则c与b相交;
④同一平面内两条直线的位置关系可能是平行或垂直;
⑤有公共顶点并且相等的角是对顶角.
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】A
【解析】解:∵同位角不一定相等,∴①错误;
∵互补或互余是两个角之间的关系,∴说∠A+∠B+∠C=180°,则∠A、∠B、∠C互补错误,∴②错误;
∵同一平面内的三条直线a、b、c,若a∥b,c与a相交,则c与b相交,∴③正确;
∵同一平面内两条直线的位置关系可能是平行或相交,∴④错误;
∵如图,
∠ABC=∠ABD,∠ABC和∠ABD有公共顶点并且相等的角,但不是对顶角,∴⑤错误;
即正确的个数是1个,
故选A.
【考点精析】掌握余角和补角的特征和对顶角和邻补角是解答本题的根本,需要知道互余、互补是指两个角的数量关系,与两个角的位置无关;两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2a2)3+2a2a4=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(0,2)在( )
A. 第二象限 B. x轴的正半轴上
C. y轴的正半轴上 D. 第四象限
-
科目: 来源: 题型:
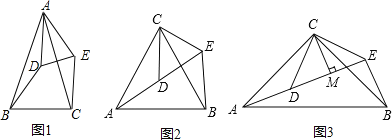
查看答案和解析>>【题目】(1)如图1,△ABC与△ADE均是顶角为40°的等腰三角形,BC、DE分别是底边,求证:BD=CE;
(2)如图2,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
填空:∠AEB的度数为 ;线段BE与AD之间的数量关系是 .
(3)拓展探究
如图3,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥EF,∠BCD=135°,∠FDC=85°,则∠B+∠F的度数为( )

A.38°
B.40°
C.55°
D.60° -
科目: 来源: 题型:
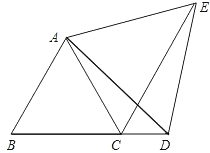
查看答案和解析>>【题目】如图,等边△ABC中,点D在延长线上,CE平分∠ACD,且CE=BD.说明:△ADE是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的内角和是540°,则这个多边形是边形.
相关试题

