搜索
【题目】等腰三角形的顶角为50°，则它的底角为 ▲ .
参考答案：
【答案】65°
【解析】据三角形内角和等于180度，用“180-50=130度”求出它的两个底角的度数，又因它是一个等腰三角形，所以它的两个底角的度数相等，用“130÷2=65度”，即可得出它的底角的度数．
解：（180-50）÷2，
=130÷2，
=65（度）；
答：它的底角有65度．
故答案为：65．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图的七边形ABCDEFG中，AB、ED的延长线相交于O点．若图中∠1、∠2、∠3、∠4的外角的角度和为220°，则∠BOD的度数为 ．
-
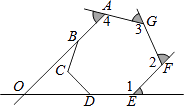
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）（﹣12）﹣5+（﹣14）﹣（﹣39）
（2）
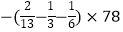
（3）
（4）
． -
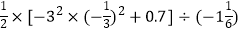科目： 来源： 题型：
查看答案和解析>>【题目】化简求值：
（1）（2a2+1﹣2a）﹣（a2﹣a+2）
（2）
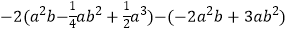
（3）化简求值：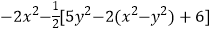
，其中x=﹣3，y=﹣ 
． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，面积为6的平行四边形纸片ABCD中，AB=3，∠BAD=45°，按下列步骤进行裁剪和拼图．
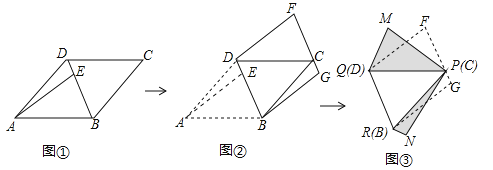
第一步：如图①，将平行四边形纸片沿对角线BD剪开，得到△ABD和△BCD纸片，再将△ABD纸片沿AE剪开（E为BD上任意一点），得到△ABE和△ADE纸片；
第二步：如图②，将△ABE纸片平移至△DCF处，将△ADE纸片平移至△BCG处；
第三步：如图③，将△DCF纸片翻转过来使其背面朝上置于△PQM处（边PQ与DC重合，△PQM和△DCF在DC同侧），将△BCG纸片翻转过来使其背面朝上置于△PRN处，（边PR与BC重合，△PRN和△BCG在BC同侧）．
则由纸片拼成的五边形PMQRN中，对角线MN长度的最小值为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连结AD．AG．
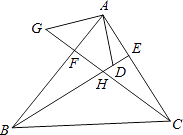
（1）求证：AD=AG；
（2）AD与AG的位置关系如何． -
科目： 来源： 题型：
查看答案和解析>>【题目】若记y=f（x）=
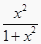，其中f（1）表示当x=1时y的值，即f（1）= 
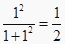；f（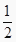 
）表示当x= 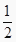时y的值，即 
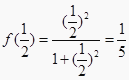；…；则f（1）+f（2）+f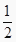（ ）+f（3）+f（ 
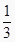）+…+f（2011）+f（ 
）=。
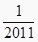相关试题
