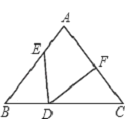
【题目】如图,△ABC中,AB=AC,BD=CF,BE=CD,∠EDF=a,则下列结论正确的是( )
A. a+∠A=90° B. a+∠A=180° C. 2a+∠A=90° D. 2a+∠A=180°
参考答案:
【答案】D
【解析】
根据已知条件可证明△BDE≌△CFD,则∠BED=∠CDF,由∠A+∠B+∠C=180°,得∠B=![]() ,因为∠BDE+∠EDF+∠CDF=180°,所以得出a与∠A的关系.
,因为∠BDE+∠EDF+∠CDF=180°,所以得出a与∠A的关系.
解:在△BDE和△CFD中,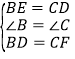 ,
,
∴△BDE≌△CFD,
∴∠BED=∠CDF,
∵∠A+∠B+∠C=180°,
∴∠B=![]() ,
,
∵∠BDE+∠EDF+∠CDF=180°,
∴180°-∠B-∠BED+a+∠CDF=180°,
∴∠B=a,
即![]() =a,
=a,
整理得2a+∠A=180°.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,路灯下一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.

(1)指定路灯的位置(用点P表示);
(2)在图中画出表示大树高的线段;
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=20°,∠2=25°,∠A=35°,求∠BDC的度数.
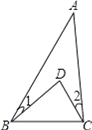
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFB=_____°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
 在图中画出与
在图中画出与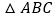 关于直线l成轴对称的
关于直线l成轴对称的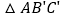 ;
;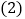 三角形ABC的面积为______;
三角形ABC的面积为______;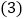 以AC为边作与
以AC为边作与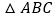 全等的三角形,则可作出______个三角形与
全等的三角形,则可作出______个三角形与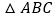 全等;
全等;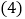 在直线l上找一点P,使
在直线l上找一点P,使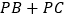 的长最短.
的长最短.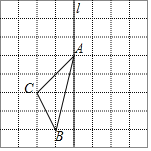
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交BC、AC于点D、E.
(1)若AC=12,BC=15,求△ABD的周长;
(2)若∠B=20°,求∠BAD的度数.

相关试题

