【题目】操作与探索:
已知点O为直线AB上一点,作射线OC,将直角三角板ODE放置在直线上方(如图①),使直角顶点与点O重合,一条直角边OD重叠在射线OA上,将三角板绕点O旋转

(1)当三角板旋转到如图②的位置时,若OD平分∠AOC,试说明OE也平分∠BOC.
(2)若OC⊥AB,垂足为点O(如图③),请直接写出与∠DOB互补的角
(3)若∠AOC=135°(如图④),三角板绕点O按顺时针从如图①的位置开始旋转,到OE边与射线OB重合结束. 请通过操作,探索:在旋转过程中,∠DOB![]() ∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
参考答案:
【答案】(1)由OD平分∠AOC可得∠AOD=∠COD,由∠DOE=90°可得∠AOD+∠EOB=90°,∠COD+∠COE=90°,即可证得结论;(2)∠AOD、∠COE;
(3)①若n≤45°,∠DOB![]() ∠COE=135°,②若n>45°,∠DOB
∠COE=135°,②若n>45°,∠DOB![]() ∠COE=225°
∠COE=225°![]() 2n
2n
【解析】
试题分析:(1)由OD平分∠AOC可得∠AOD=∠COD,由∠DOE=90°可得∠AOD+∠EOB=90°,∠COD+∠COE=90°,即可证得结论;
(2)由OC⊥AB可得∠AOD+∠COD=90°,由∠DOE=90°可得∠COD+∠COE=90°,即可得到∠AOD=∠COE,从而可以求得与∠DOB互补的角;
(3)由于旋转45°时,OE与OC重合,故要分n≤45°与n>45°两种情况分析.
(1)∵OD平分∠AOC
∴∠AOD=∠COD
∵∠DOE=90°
∴∠AOD+∠EOB=90°,∠COD+∠COE=90°
∴∠COE=∠EOB
∴OE也平分∠BOC;
(2)∵OC⊥AB,∠DOE=90°
∴∠AOD+∠COD=90°,∠COD+∠COE=90°
∴∠AOD=∠COE
∴与∠DOB互补的角为∠AOD、∠COE;
(3)①若n≤45°,∠DOB![]() ∠COE=(180°-n)-(45°-n)=180°-n-45°+n=135°,
∠COE=(180°-n)-(45°-n)=180°-n-45°+n=135°,
②若n>45°,∠DOB![]() ∠COE=(180°-n)-(n-45°)=180°-n-n+45°=225°
∠COE=(180°-n)-(n-45°)=180°-n-n+45°=225°![]() 2n.
2n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.
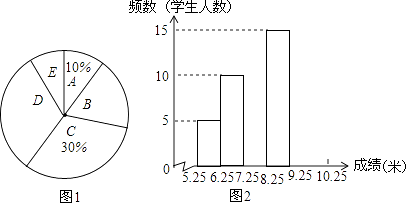
(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率. -
科目: 来源: 题型:
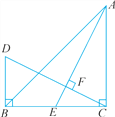
查看答案和解析>>【题目】如图,在△ABC中,点D是AB的中点,点F是BC延长线上一点,连接DF,交AC于点E,连接BE,∠A=∠ABE.
(1)求证:DF是线段AB的垂直平分线;
(2)当AB=AC,∠A=46°时,求∠EBC及∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我镇绿色和特色农产品在市场上颇具竞争力.外贸商胡经理按市场价格10元/千克在我区收购了6000千克蘑菇存放入冷库中.请根据胡经理提供的预测信息(如图)帮胡经理解决以下问题:

(1)若胡经理想将这批蘑菇存放x天后一次性出售, 则x天后这批蘑菇的销售单价为元, 这批蘑菇的销售量是千克;
(2)胡经理将这批蘑菇存放多少天后,一次性出售所得的销售总金额为100000元;(销售总金额=销售单价×销售量).
(3)将这批蘑菇存放多少天后一次性出售可获得最大利润?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作AE 的垂线CF,垂足为F,过点B作BD⊥BC,交CF的延长线于点D.
(1)求证:AE=CD.
(2)若AC=12 cm,求BD的长.
-
科目: 来源: 题型:
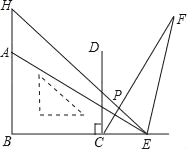
查看答案和解析>>【题目】如图,点A、C分别在一个含45°的直角三角板HBE的两条直角边BH和BE上,且BA=BC,过点C作BE的垂线CD,过E点作EF⊥AE交∠DCE的角平分线于F点,交HE于P.
(1)试判断△PCE的形状,并请说明理由;
(2)若∠HAE=120°,AB=3,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)
为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动.学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:


请根据图表信息回答下列问题:
(1)频数分布表中的
 ,
,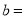 ;
;(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在
 小时以上的学生评为“阅读之星”,请你估计该校
小时以上的学生评为“阅读之星”,请你估计该校 名学生中评为“阅读之星”的有多少人?
名学生中评为“阅读之星”的有多少人?
相关试题

