Question

【题目】直线y=﹣ x+3和x轴、y轴的交点分别为B、C，点A的坐标是（﹣ ，0），另一条直线经过点A、C．

（1）求线段AC所对应的函数表达式；
（2）动点M从B出发沿BC运动，速度为1秒一个单位长度．当点M运动到C点时停止运动．设M运动t秒时，△ABM的面积为S．
①求S与t的函数关系式；
②当t为何值时，S= S△ABC ， （注：S△ABC表示△ABC的面积），求出对应的t值；
③当t=4的时候，在坐标轴上是否存在点P，使得△BMP是以BM为直角边的直角三角形？若存在，请直接写出P点坐标，若不存在，请说明理由．

Answer 1

【答案】
（1）

解：当y=0时，﹣ x+3=0，解得x=3 ，即B（3 ，0）

当x=0时，y=3，即C点坐标是（0，3）

设线段AC所对应的函数表达式y=kx+b，图象经过A、C点，得 ，

解得 ．

故线段AC所对应的函数表达式y= x+3

（2）

解：如图1，

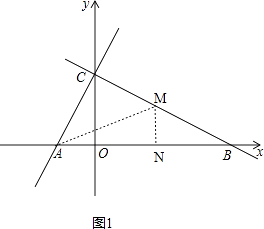
①由动点M从B出发沿BC运动，速度为1秒一个单位长度，行驶t秒，得BM=t，

由线段的和差，得AB=3 ﹣（﹣ ）=4 ，

由正切函数，得tan∠B= = = ，∠ABC=30°，

由正弦函数，得MD=BMsin∠ABC= t．

由三角形面积公式，得S= ABMD= × t×4 = t

即S= t；

②由S= S△ABC，得MD= OC= ，即 t= ，解得t=3，

当t=3时，S= S△ABC；

③如图2：

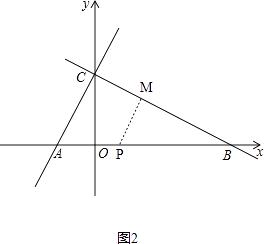
当t=4时，在坐标轴上存在点P，使得△BMP是以BM为直角边的直角三角形，

(i)如图2，

∵点M运动的速度为每秒1个单位长度，

∴当t=4时，BM=4，

∵∠ABC=30°，∠PMB=90°，

∴BP=BM÷cos30°=4÷ = ，

∴OP=OB﹣BP=3 ﹣ = ，

∴点P的坐标是（ ，0）．

(ii)如图3，

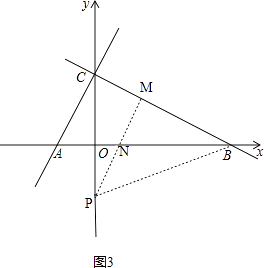
PM和AB相交于点N，，

∵点M运动的速度为每秒1个单位长度，

∴当t=4时，BM=4，

∵∠ABC=30°，∠NMB=90°，

∴BN=BM÷cos30°=4÷ = ，

∴ON=OB﹣BN=3 ﹣ = ，

∵∠MNB=90°﹣30°=60°，∠ONP=∠MNB，

∴∠ONP=60°，

∴OP=ONtan60°= =1，

∴点P的坐标是（0，﹣1）．

(iii)如图4，

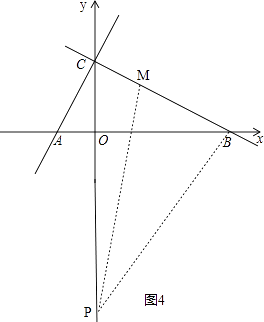
∵OC=3，∠ABC=30°，∠BOC=90°，

∴BC=2×3=6，∠PCB=90°﹣30°=60°，

又∵∠PBC=90°，

∴∠BPC=90°﹣60°=30°，

∴CP=2BC=2×6=12，

∴OP=CP﹣OC=12﹣3=9，

∴点P的坐标是（0，﹣9）．

综上，可得

当t=4时，在坐标轴上存在点P，使得△BMP是以BM为直角边的直角三角形，

点P的坐标是（ ，0）、（0，﹣1）或（0，﹣9）．

【解析】（1）根据函数值，可得相应自变量的值，根据自变量的值，可得相应的函数值，根据待定系数法，可得函数解析式；（2）①根据M的运动时间及运动速度，可得BM的长，根据正切函数值，可得∠B的大小，再根据正弦函数，可得MD的长，根据线段的和差，可得AB的长，根据三角形的面积公式，可得答案；②根据等底三角形面积间的S= S△ABC的关系，可得MD= OB，可得答案；③根据题意，分三种情况：①点P在x轴上时；②点P在y轴上，且BP为斜边时；③点P在y轴上，且BP为另一条直角边时；然后根据直角三角形的性质分类讨论，求出P点坐标各是多少即可．
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识，掌握一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小．