【题目】已知:在Rt△ABC中,∠C=90°∠A、∠B、∠C所对的边分别记作a、b、c.
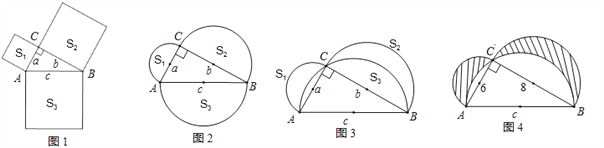
(1)如图1,分别以△ABC的三条边为边长向外作正方形,其正方形的面积由小到大分别记作S1、S2、S3,则有____________;
(2)如图2,分别以△ABC的三条边为直径向外作半圆,其半圆的面积由小到大分别记作S1、S2、S3,请问S1+S2与S3有怎样的数量关系,并证明你的结论;
(3)分别以直角三角形的三条边为直径作半圆,如图3所示,其面积由小到大分别记作S1、S2、S3,根据(2)中的探索,直接回答S1+S2与S3有怎样的数量关系;
(4)若Rt△ABC中,AC=6,BC=8,求出图4中阴影部分的面积.
参考答案:
【答案】(1)S1+S2=S3;(2)![]() ;(3)
;(3)![]() ;(4)24cm
;(4)24cm![]() .
.
【解析】试题分析:(1)根据勾股定理即可得到a,b,c满足的关系.
(2)根据正方形的面积公式结合勾股定理就可发现大正方形的面积是两个小正方形的面积和;
(3)分别表示出S1、S2、S3,结合勾股定理即可得出关系式.
(4)根据半圆的面积公式以及勾股定理就可发现:两个小半圆的面积和等于大半圆的面积,从而得出阴影部分的面积=直角三角形的面积.
试题解析:(1)根据勾股定理可得S1+S2=S3.
(2)由题意得,S1=b2,S2=a2,S3=c2,∵a2+b2=c2,∴S1+S2=S3.
(3)S1=![]() ×b2,S2=
×b2,S2=![]() ×a2,S3=
×a2,S3=![]() ×c2,∵a2+b2=c2,∴S1+S2=S3.
×c2,∵a2+b2=c2,∴S1+S2=S3.
(4)因为a2+b2=c2,两边同乘以![]() ,即得两小半圆的面积和等于大半圆的面积,
,即得两小半圆的面积和等于大半圆的面积,
从而可得S阴影部分的面积=S直角三角形的面积=![]() ×8×6=24.故阴影部分的面积是24.
×8×6=24.故阴影部分的面积是24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织学生到生态园春游,某班学生9:00从樱花园出发,匀速前往距樱花园2 km的桃花园.在桃花园停留1 h后,按原路返回樱花园,返程中先按原来的速度行走了6 min,随后接到通知,要尽快回到樱花园,故速度提高到原来的2倍,于10:48回到了樱花园,求这班学生原来的行走速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明:“若整数系数一元二次方程ax2+bx+c=0(a≠0)有有理根,则a,b,c中至少有一个是偶数”,下列假设中正确的是( )
A. 假设a,b,c都是偶数 B. 假设a,b,c都不是偶数
C. 假设a,b,c至多有一个是偶数 D. 假设a,b,c至多有两个是偶数
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣4= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).此时EC有多长?

-
科目: 来源: 题型:
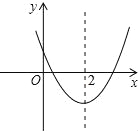
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:
①abc<0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0
其中正确结论的有( )
A.①②③ B.①②④ C.①③④ D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3a2﹣a﹣2=0,则5+2a﹣6a2= .
相关试题

