【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).此时EC有多长?

参考答案:
【答案】3
【解析】试题分析:根据题意,在Rt△FCE中,利用勾股定理求出EC长,设EC为x,因为△ADE与△AFE对折,所以 EF=DE=8-x, AF=AD=10, 在Rt△ABF中,利用勾股定理能求出BF=6,所以FC=4, 在Rt△FCE中, 利用勾股定理可求出EC.
试题解析:根据题意,设EC为x ,∵△ADE与△AFE对折,
∴EF=DE=8-x,Rt△ABF中,AF=AD=10,AB=8,BF2=AF2-AB2,
∴BF=6,∴FC=BC-BF=10-6=4,在Rt△FCE中,EC=x,EF=8-x,FC=4,
∴(8-x)2=x2+42,解得:x=3,即EC=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明:“若整数系数一元二次方程ax2+bx+c=0(a≠0)有有理根,则a,b,c中至少有一个是偶数”,下列假设中正确的是( )
A. 假设a,b,c都是偶数 B. 假设a,b,c都不是偶数
C. 假设a,b,c至多有一个是偶数 D. 假设a,b,c至多有两个是偶数
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣4= .
-
科目: 来源: 题型:
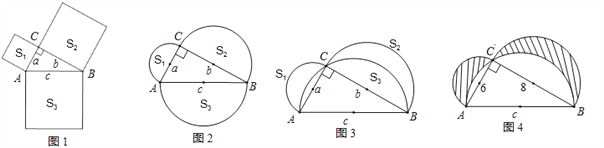
查看答案和解析>>【题目】已知:在Rt△ABC中,∠C=90°∠A、∠B、∠C所对的边分别记作a、b、c.
(1)如图1,分别以△ABC的三条边为边长向外作正方形,其正方形的面积由小到大分别记作S1、S2、S3,则有____________;
(2)如图2,分别以△ABC的三条边为直径向外作半圆,其半圆的面积由小到大分别记作S1、S2、S3,请问S1+S2与S3有怎样的数量关系,并证明你的结论;
(3)分别以直角三角形的三条边为直径作半圆,如图3所示,其面积由小到大分别记作S1、S2、S3,根据(2)中的探索,直接回答S1+S2与S3有怎样的数量关系;
(4)若Rt△ABC中,AC=6,BC=8,求出图4中阴影部分的面积.
-
科目: 来源: 题型:
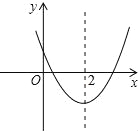
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:
①abc<0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0
其中正确结论的有( )
A.①②③ B.①②④ C.①③④ D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3a2﹣a﹣2=0,则5+2a﹣6a2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若单项式3x2m﹣1y5与单项式﹣5x3yn是同类项,则m,n的值分别为( )
A. 3,5B. 2,3C. 2,5D. 3,﹣2
相关试题

