【题目】如图①,南京中山陵的台阶拾级而上被分成坡度不等的两部分.图②是台阶的侧面图,若斜坡BC长为120m,在C处看B处的仰角为25°;斜坡AB长70m,在A处看B处的俯角为50°,试求出陵墓的垂直高度AE的长.
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47)

考点:解直角三角形的应用-仰角俯角问题.
参考答案:
【答案】
【解析】
试题分析:在Rt△BDC中,根据sinC=![]() ,求出BD的长,然后在Rt△AFB中,根据sin∠ABF=
,求出BD的长,然后在Rt△AFB中,根据sin∠ABF=![]() ,求出AF的长,进而求出AE的长.
,求出AF的长,进而求出AE的长.
解:在Rt△BDC中,sinC=![]() ,
,
∴BD=BCsinC=BCsin25°=120×0.42=50.4 m.
在Rt△AFB中,sin∠ABF=![]() ,
,
∴AF=ABsin∠ABF=ABsin50°=70×0.77=53.9 m.
∴AE=AF+FE=AF+BD=50.4+53.9=104.3m.
答:陵墓的垂直高度AE的长为104.3 m.
-
科目: 来源: 题型:
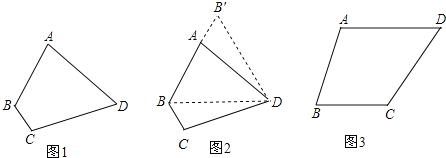
查看答案和解析>>【题目】【问题提出】如图1,四边形ABCD中,AD=CD,∠ABC=120°,∠ADC=60°,AB=2,BC=1,求四边形ABCD的面积.
【尝试解决】
旋转是一种重要的图形变换,当图形中有一组邻边相等时,往往可以通过旋转解决问题.
(1)如图2,连接 BD,由于AD=CD,所以可将△DCB绕点D顺时针方向旋转60°,得到△DAB′,则△BDB′的形状是 .
(2)在(1)的基础上,求四边形ABCD的面积.
[类比应用]如图3,四边形ABCD中,AD=CD,∠ABC=75°,∠ADC=60°,AB=2,BC=
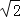 ,求四边形ABCD的面积.
,求四边形ABCD的面积.考点:几何变换综合题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市“艺术节”期间,小明、小亮都想去观看茶艺表演,但是只有一张茶艺表演门票,他们决定采用抽卡片的办法确定谁去.规则如下:
将正面分别标有数字1、2、3、4的四张卡片(除数字外其余都相同)洗匀后,背面朝上放置在桌面上,随机抽出一张记下数字后放回;重新洗匀后背面朝上放置在桌面上,再随机抽出一张记下数字.如果两个数字之和为奇数,则小明去;如果两个数字之和为偶数,则小亮去.
(1)请用列表或画树状图的方法表示抽出的两张卡片上的数字之和的所有可能出现的结果;
(2)你认为这个规则公平吗?请说明理由.
考点:游戏公平性;列表法与树状图法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市少体校为了从甲、乙两名运动员中选出一名运动员参加省运动会百米比赛,组织了选拔测试,分别对两人进行了五次测试,成绩(单位:秒)以及平均数、方差如表:
甲
13
13
14
16
18
x
 =14.8
=14.8S
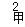 =3.76
=3.76乙
14
14
15
15
16
x
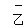 =14.8
=14.8S
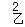 =0.56
=0.56学校决定派乙运动员参加比赛,理由是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
(1)求线段CD对应的函数表达式;
(2)求E点的坐标,并解释E点的实际意义;
(3)若已知轿车比货车晚出发20分钟,且到达乙地后在原地等待货车,在两车相遇后当货车和轿车相距30千米时,求货车所用时间.

考点:一次函数的应用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组线段为边,能组成三角形的是( )
A. 3cm.4cm.8cm
B. 8cm,7cm,15cm
C. 5cm,5cm,11cm
D. 11cm,12cm,13crn
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a是一个三位数,现在把1放在它的右边,得到一个四位数,这个四位数是( )
A. 1000a+1 B. 100a+1 C. 10a+1 D. a+1
相关试题

