【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.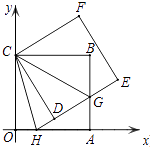
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,当G点在何位置时四边形AEBD是矩形?请说明理由并求出点H的坐标.
参考答案:
【答案】
(1)
证明:∵将正方形ABCO绕点C逆时针旋转角度α,
∴DC=CO,∠CDG=∠COA=90°,
∵四边形OCBA是正方形,
∴CB=CO,∠B=90°,
∴CB=CD,∠B=∠CDG=90°
在Rt△CDG与Rt△CBG中,
![]() ,
,
∴Rt△CDG≌Rt△CBG
(2)
解:∵∠CDG=90°,
∴∠CDH=90°,
在Rt△COH与Rt△CDH中,
![]() ,
,
∴Rt△COH≌Rt△CDH,
∴∠OCH=∠DCH,HO=DH,
∵Rt△CDG≌Rt△CBG,
∴∠DCG=∠BCG,DG=BG,
∴∠HCG=∠DCG+∠DCH=45°,
HG=HD+DG=HO+BG
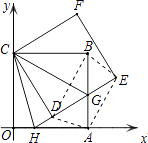
(3)
解:当G是AB中点时,四边形ADBE是矩形,
∵G是AB中点,
∴BG=AG= ![]() AB
AB
由(2)得DG=BG,
又∵AB=DE,
∴DG= ![]() DE,
DE,
∴DG=GE=BG=AG,
∴四边形AEBD是平行四边形,
∵AB=DE,
∴□ADBE是矩形,
设点H的坐标为(x,0),
则HO=HD=x,DG=BG=AG=3,AH=6﹣x,
由勾股定理得,(6﹣x)2+33=(3+x)2,
解得,x=2,
∴H(2,0).
【解析】(1)根据旋转变换的性质得到DC=CO,∠CDG=∠COA=90°,根据正方形的性质得到CB=CO,∠B=90°,根据直角三角形的全等的判定定理证明即可;(2)证明Rt△COH≌Rt△CDH,得到∠OCH=∠DCH,HO=DH,等量代换即可;(3)根据矩形的判定定理证明四边形AEBD是矩形,设点H的坐标为(x,0),根据勾股定理列出方程,解方程求出x的值,得到点H的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式3x2y的系数为
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(a,-b)在第二象限内,则点(-a,-b)在第________象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列解题过程:
计算:1+5+52+53+…+524+525的值.
解:设S=1+5+52+53+…+524+525 , ⑴
则5S=5+52+53+…+525+526⑵
⑵﹣⑴,得4S=526﹣1
S=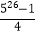
通过阅读,你一定学会了一种解决问题的方法,请用你学到的方法计算:
(1)1+3+32+33+…+39+310
(2)1+x+x2+x3+…+x99+x100 . -
科目: 来源: 题型:
查看答案和解析>>【题目】若点M在第一、三象限的角平分线上,且点M到x轴的距离为2,则点M的坐标是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小华认为在多项式2x2+3x+1中一定有因式(x+1),他是这样想的:2x2+3x+1=2x2+2x+x+1=2x(x+1)+(x+1)=(x+1)(2x+1).你认为他这样做有道理吗?如果你认为有道理,试着看看x2+3x+2中有没有因式(x+1);如果你认为没有道理,试说出其中的错误所在.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(-2)2019+(-2)2018的结果.
相关试题

