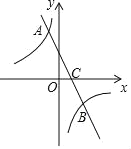
【题目】如图,直线y=kx+b(k≠0)与双曲线y=![]() (m≠0)交于点A(
(m≠0)交于点A(![]() ,2)B(1,﹣1).
,2)B(1,﹣1).
(1)方程kx+b﹣![]() =0的解为 ,不等式
=0的解为 ,不等式![]() 的解集是 ;(请直接写出答案)
的解集是 ;(请直接写出答案)
(2)点P在x轴上,如果S△ABP=3,求点P的坐标.
参考答案:
【答案】(1)x=﹣![]() 或1;﹣
或1;﹣![]() <x<0或x>1;(2)点P的坐标为(﹣
<x<0或x>1;(2)点P的坐标为(﹣![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)结合图象,分析函数值的大小关系即可;(2)用待定系数法求直线解析式;设点P的坐标为(x,0),则PC=|x﹣![]() |,根据面积公式求解.
|,根据面积公式求解.
解:(1)当x=﹣![]() 或x=1时,kx+b=
或x=1时,kx+b=![]() ,所以方程kx+b﹣
,所以方程kx+b﹣![]() =0的解为x=﹣
=0的解为x=﹣![]() 或1;
或1;
当﹣![]() <x<0或x>1时,kx+b<
<x<0或x>1时,kx+b<![]() ,则不等式kx+b<
,则不等式kx+b<![]() 的解集是﹣
的解集是﹣![]() <x<0或x>1;
<x<0或x>1;
故答案为x=﹣![]() 或1;﹣
或1;﹣![]() <x<0或x>1;
<x<0或x>1;
(2)把A(![]() ,2)B(1,﹣1)代入y=kx+b得
,2)B(1,﹣1)代入y=kx+b得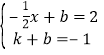 ,解得
,解得![]() ,则直线解析式为y=﹣2x﹣1,
,则直线解析式为y=﹣2x﹣1,
当x=0时,﹣2x+1=0,解得x=![]() ,则C(
,则C(![]() ,0),
,0),
设点P的坐标为(x,0),则PC=|x﹣![]() |,
|,
∵S△ABP=3,
∴![]() ×3|x﹣
×3|x﹣![]() |=3,即|x﹣
|=3,即|x﹣![]() |=2,
|=2,
解得:x1=﹣![]() ,x2=
,x2=![]() ,
,
∴点P的坐标为(﹣![]() ,0)或(
,0)或(![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度
2013
2014
2015
2016
投入技改资金
 (万元)
(万元)2.5
3
4
4.5
产品成本
 (万元/件)
(万元/件)7.2
6
4.5
4
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:
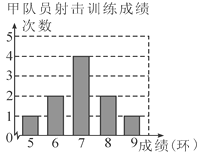

根据以上信息,整理分析数据如下:
平均成绩(环)
中位数(环)
众数(环)
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
-
科目: 来源: 题型:
查看答案和解析>>【题目】刚刚升入初一,学习成绩优异但体育一般的王晴同学未雨绸缪,已经为将来的体育中考做起了准备.上周末她在家练习1分钟跳绳,以每分钟150下为基准,超过或不足的部分分别用正负数来表示,8次成绩(单位:下)分别是-10,-8,-5,-2,+2,+8,+3,-4.
(1)成绩最好的一次比最差的一次多跳多少下?
(2)求王晴这8次跳绳的平均成绩.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某销售商准备在南充采购一批丝绸,经调查,用10000元采购A型丝绸的件数与用8000元采购B型丝绸的件数相等,一件A型丝绸进价比一件B型丝绸进价多100元.
(1)求一件A型、B型丝绸的进价分别为多少元?
(2)若销售商购进A型、B型丝绸共50件,其中A型的件数不大于B型的件数,且不少于16件,设购进A型丝绸m件.
①求m的取值范围.
②已知A型的售价是800元/件,销售成本为2n元/件;B型的售价为600元/件,销售成本为n元/件.如果50≤n≤150,求销售这批丝绸的最大利润w(元)与n(元)的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=x+b的图象经过点A(﹣2,0),与反比例函数y=
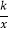 (x>0)的图象交于B(a,4).
(x>0)的图象交于B(a,4).(1)求一次函数和反比例函数的表达式;
(2)设M(m﹣2,m)是直线AB上一点,过M作MN∥x轴,交反比例函数y=
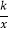 (x>0)的图象于点N,若AONM为顶点的四边形为平行四边形,求点M的坐标.
(x>0)的图象于点N,若AONM为顶点的四边形为平行四边形,求点M的坐标.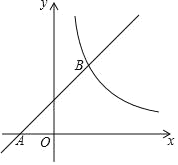
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c所表示的数在数轴上的位置如图所示:

(1)化简:│a-1│-│c+b│+│b-1│;
(2)若a+b+c=0,且b与-1的距离和c与-1的距离相等,求:-a2+2b-c-(a-4c-b)的值.
相关试题

