【题目】“脐橙结硕果,香飘引客来”,赣南脐橙以其“外表光洁美观,肉质脆嫩,风味浓甜芳香”的特点饮誉中外.现欲将一批脐橙运往外地销售,若用2辆A型车和1辆B型车载满脐橙一次可运走10吨;用1辆A型车和2辆B型车载满脐橙一次可运走11吨.现有脐橙31吨,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满脐橙.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满脐橙一次可分别运送多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若1辆A型车需租金100元/次,1辆B型车需租金120元/次.请选出费用最少的租车方案,并求出最少租车费.
参考答案:
【答案】(1)1辆A型车装满货物一次可运3吨,1辆B型车装满货物一次可运4吨;
(2)一共有有3种租车方案:方案一:租A型车1辆,B型车7辆; 方案二:租A型车5辆,B型车4辆;方案三:租A型车9辆,B型车1辆;
(3)最省钱的租车方案是方案三,即租A型车1辆,B型车7辆,最少租车费为940元.
【解析】
(1)根据“用2辆A型车和1辆B型车载满脐橙一次可运走10吨;用1辆A型车和2辆B型车载满脐橙一次可运走11吨”列出方程组,解方程组即可得出答案;
(2)结合(1)和“现有脐橙31吨”列出方程,解方程即可得出答案;
(3)根据(2)的方案分别计算每种方案的运费,取最低运费即可得出答案.
解:(1)设每辆A型车、B型车都装满货物一次可以分别运货x吨、y吨,
依题意列方程组得:![]()
解得![]()
答:1辆A型车装满货物一次可运3吨,1辆B型车装满货物一次可运4吨。
(2)结合题意和(1)得:3a+4b=31
∵a、b都是正整数
![]() 或
或![]() 或
或![]()
所以一共有有3种租车方案:
方案一:租A型车1辆,B型车7辆;
方案二:租A型车5辆,B型车4辆; .
方案三:租A型车9辆,B型车1辆. .
(3)因为A型车每辆需租金100元/次,B型车每辆需租金120元/次,
所以方案一需租金:1×100+7×200=940(元);
方案二需租金:5×100+4×120=980(元);
方案三需租金:9×100+1×120=1020(元).
∵1020>980>940
∴最省钱的租车方案是方案三,即租A型车1辆,B型车7辆,最少租车费为940元
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x
﹣1
0
1
3
y
﹣1
3
5
3
下列结论:
①ac<0; ②当x>1时,y的值随x值的增大而减小;
③当 时,
时,  ; ④3是方程ax2+(b﹣1)x+c=0的一个根.
; ④3是方程ax2+(b﹣1)x+c=0的一个根.
其中正确的结论是(填正确结论的序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三个项点的坐标分别为A (3. 3),B (-3, 0), C (0. -2).
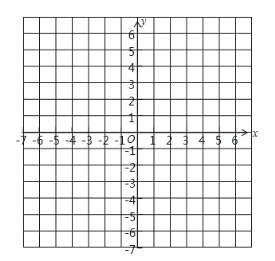
(1)在下面的平面直角坐标系中分别描出A,B, C三点,并画出△ABC;
(2)将(1)中的△ABC向上平移3个单位长度,向左中移2个单位长度,得到△
 在图中画出△
在图中画出△ ,请分别写出A1、B1、C1三点的坐标.
,请分别写出A1、B1、C1三点的坐标.(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016甘肃省白银市)如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.

-
科目: 来源: 题型:
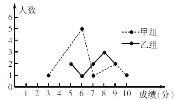
查看答案和解析>>【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀. 为了解本次大赛的成绩,校团委随机抽取了甲、乙两组学生成绩作为样本进行统计,绘制了如下统计图表:
组别
平均数
中位数
方差
合格率
优秀率
甲组
6.8
a
3.76
90%
30%
乙组
b
7.5
1.96
80%
20%
(1)求出表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面的表格判断,小英属于哪个组?
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组. 但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 :y=2x+1与直线
:y=2x+1与直线 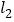 :y=mx+4相交于点P(1,b)
:y=mx+4相交于点P(1,b)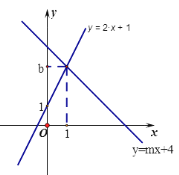
(1)求b,m的值
(2)垂直于x轴的直线 x=a与直线
 ,
,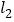 分别相交于C,D,若线段CD长为2,求a的值
分别相交于C,D,若线段CD长为2,求a的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列解答过程,然后再解题.
例:已知多项式2x3﹣x2+m有一个因式是2x+1,求m的值.
解法一:设2x3﹣x2+m=(2x+1)(x 2+ax+b),
则2x 3﹣x2+m=2x 3+(2a+1)x2+(a+2b)x+b.
比较系数得
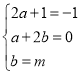 ,解得
,解得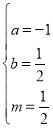 ,∴m=
,∴m=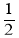 .
.解法二:设2x3﹣x2+m=A(2x+1)(A为整式)
由于上式为恒等式,为方便计算了取x=﹣
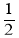 ,2×(﹣)3﹣(﹣)2+m=0,故m=
,2×(﹣)3﹣(﹣)2+m=0,故m=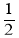 .
.(1)已知多项式2x3﹣2x2+ m有一个因式是x+2,求m的值.
(2)已知x 4+ m x3+ n x﹣16有因式(x﹣1)和(x﹣2),求m、n的值.
相关试题

