【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(7,3),点E在边AB上,且AE=1,已知点P为y轴上一动点,连接EP,过点O作直线EP的垂线段,垂足为点H,在点P从点F(0, ![]() )运动到原点O的过程中,点H的运动路径长为 .
)运动到原点O的过程中,点H的运动路径长为 . 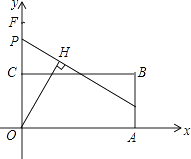
参考答案:
【答案】![]()
【解析】解:连接OE. 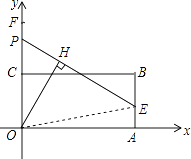
S△OPE= ![]() ×
× ![]() ×7=
×7= ![]() ,
,
在直角△OEA中,OE= ![]() =
= ![]() =
= ![]() =5
=5 ![]() ,
,
PE= ![]() =
= ![]() ,
,
∵S△OPE= ![]() PEOH,即
PEOH,即 ![]() ×
× ![]() OH=
OH= ![]() ,
,
∴OH=5,
∴在直角△OEH中,sin∠OEH= ![]() =
= ![]() =
= ![]() ,
,
∴∠OEH=45°,
点H的运动路径长是: ![]() =
= ![]() .
.
故答案是: ![]() .
.
H经过的路径是以OE为直径的弧,连接OE,首先求得△OPE的面积,然后利用三角形面积公式求得OH的长,然后在直角△OEH中,利用三角函数求得∠OEH的度数,然后利用长公式即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一个新的运算:a⊕b=
 ,则运算x⊕2的最小值为( )
,则运算x⊕2的最小值为( )
A.﹣3
B.﹣2
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
①当x=1时,点P是正方形ABCD的中心;
②当x= 时,EF+GH>AC;
时,EF+GH>AC;
③当0<x<2时,六边形AEFCHG面积的最大值是3;
④当0<x<2时,六边形AEFCHG周长的值不变.
其中正确的选项是( )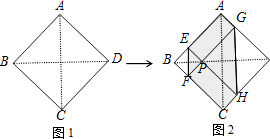
A.①③
B.①②④
C.①③④
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个瓶子的容积为1 L,瓶内装着溶液,当瓶子正放时,瓶内溶液的高度为20 cm,当瓶子倒放时,空余部分的高度为5 cm.现把瓶内的溶液全部倒在一个圆柱形的杯子里,杯内的溶液高度为10 cm.
求:(1)瓶内溶液的体积;
(2)圆柱形杯子的内底面半径(π取3.14,结果精确到0.1 cm).

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1) +(
+(  )﹣1﹣2cos60°;
)﹣1﹣2cos60°;
(2)(2x﹣y)2﹣(x+y)(x﹣y). -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程与方程组
(1)解方程:x2﹣6x﹣6=0;
(2)解不等式组: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.
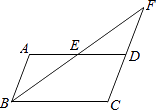
(1)证明:FD=AB;
(2)当ABCD的面积为8时,求△FED的面积.
相关试题

