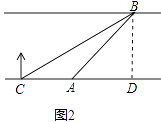
【题目】如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向,如图2.
(1)求∠CBA的度数.
(2)求出这段河的宽(结果精确到1m,备用数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73).
≈1.73).
参考答案:
【答案】
(1)解:由题意得,∠BAD=45°,∠BCA=30°,
∴∠CBA=∠BAD﹣∠BCA=15°
(2)解:作BD⊥CA交CA的延长线于D,
设BD=xm,
∵∠BCA=30°,
∴CD= ![]() =
= ![]() x,
x,
∵∠BAD=45°,
∴AD=BD=x,
则 ![]() x﹣x=60,
x﹣x=60,
解得x= ![]() ≈82,
≈82,
答:这段河的宽约为82m.
【解析】本题考查的是解直角三角形的应用﹣方向角问题,正确标注方向角、熟记锐角三角函数的定义是解题的关键.(1)根据三角形的外角的性质、结合题意计算即可;(2)作BD⊥CA交CA的延长线于D,设BD=xm,根据正切的定义用x表示出CD、AD,根据题意列出方程,解方程即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.

(1)当∠AOB=18°时,求所作圆的半径;(结果精确到0.01cm)
(2)保持∠AOB=18°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度.(结果精确到0.01cm)
(参考数据:sin9°≈0.1564,cos9°≈0.9877,sin18°≈0.3090,cos18°≈0.9511,可使用科学计算器) -
科目: 来源: 题型:
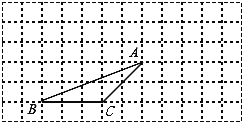
查看答案和解析>>【题目】如图,△ABC的顶点都在方格纸的格点上,将△ABC向右平移4格,再向上平移2格,其中每个格子的边长为1个单位长度。
⑴在图中画出平移后的△A′B′C′;
⑵若连接AA′、CC′,则这两条线段的关系是 ;
⑶作△ABC的高AD,并求△ABC的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.
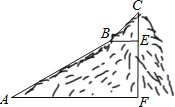
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.(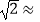 1.414,CF结果精确到米)
1.414,CF结果精确到米) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在大楼AB的正前方有一斜坡CD,已知斜坡CD长6
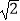 米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.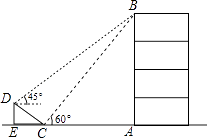
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 为
为 的高,
的高,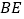 是
是 的角平分线,若
的角平分线,若 ,
,
(1)求
 的度数;
的度数;(2)若点F为线段
 上任一点,当
上任一点,当 为直角三角形时,求
为直角三角形时,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】提出问题:
(1)如图,我们将图(1)所示的凹四边形称为“镖形”.在“镖形”图中,
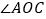 与
与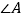 、
、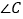 、
、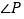 的数量关系为____.
的数量关系为____.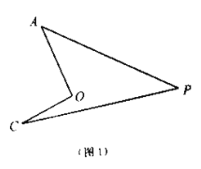
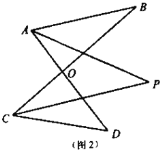
(2)如图(2),已知
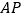 平分
平分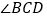 ,
,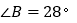 ,
,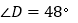 ,求
,求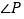 的度数.
的度数.由(1)结论得:
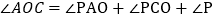
所以
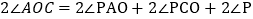 即
即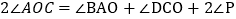
因为
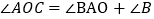
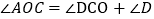
所以
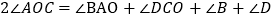
所以
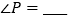 .
.解决问题:
(1)如图(3),直线
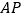 平分
平分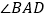 ,
, 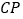 平分
平分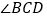 的外角
的外角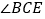 ,猜想
,猜想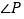 与
与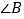 、
、 的数量关系是______;
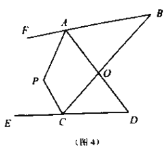
的数量关系是______;(2)如图(4),直线
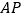 平分
平分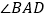 的外角
的外角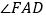 ,
, 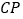 平分
平分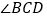 的外角
的外角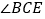 ,猜想
,猜想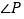 与
与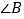 、
、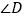 的数量关系,并说明理由.
的数量关系,并说明理由.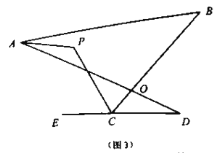
相关试题

