【题目】如图,在大楼AB的正前方有一斜坡CD,已知斜坡CD长6 ![]() 米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.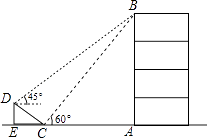
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号).
参考答案:
【答案】
(1)
解:在Rt△DCE中,DC=6 ![]() 米,∠DCE=30°,∠DEC=90°,
米,∠DCE=30°,∠DEC=90°,
∴DE=EC=6米;
(2)
解:过D作DF⊥AB,交AB于点F,
∵∠BFD=90°,∠BDF=45°,
∴∠BFD=45°,即△BFD为等腰直角三角形,则DF=BF,
设AB=x米,则BF=(x﹣6)米.
∵四边形DEAF为矩形,
∴AF=DE=6米,即AB=BF=(x﹣6)米,AC=(x﹣12)米,
在Rt△ABC中,∠ABC=30°,
tan30°= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:x=18+6 ![]() ,
,
即大楼的高度是18+6 ![]() 米.
米.
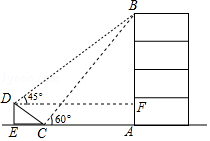
【解析】(1)在直角三角形DCE中,利用锐角三角函数定义求出DE的长即可;(2)过D作DF垂直于AB,交AB于点F,可得出三角形BDF为等腰直角三角形,设AB=x米,则BF=(x﹣6)米,AC=(x﹣12)米,在Rt△ABC中,利用三角函数即可列方、方程求得x的值.
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.
-
科目: 来源: 题型:
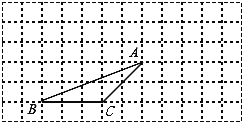
查看答案和解析>>【题目】如图,△ABC的顶点都在方格纸的格点上,将△ABC向右平移4格,再向上平移2格,其中每个格子的边长为1个单位长度。
⑴在图中画出平移后的△A′B′C′;
⑵若连接AA′、CC′,则这两条线段的关系是 ;
⑶作△ABC的高AD,并求△ABC的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.
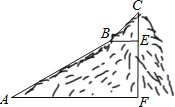
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.(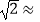 1.414,CF结果精确到米)
1.414,CF结果精确到米) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向,如图2.

(1)求∠CBA的度数.
(2)求出这段河的宽(结果精确到1m,备用数据 ≈1.41,
≈1.41,  ≈1.73).
≈1.73). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 为
为 的高,
的高,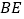 是
是 的角平分线,若
的角平分线,若 ,
,
(1)求
 的度数;
的度数;(2)若点F为线段
 上任一点,当
上任一点,当 为直角三角形时,求
为直角三角形时,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】提出问题:
(1)如图,我们将图(1)所示的凹四边形称为“镖形”.在“镖形”图中,
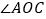 与
与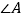 、
、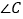 、
、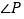 的数量关系为____.
的数量关系为____.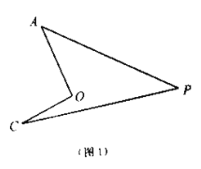
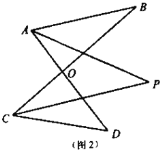
(2)如图(2),已知
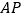 平分
平分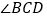 ,
,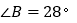 ,
,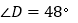 ,求
,求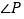 的度数.
的度数.由(1)结论得:
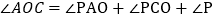
所以
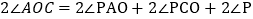 即
即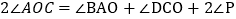
因为
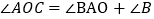
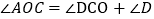
所以
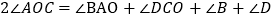
所以
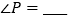 .
.解决问题:
(1)如图(3),直线
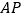 平分
平分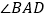 ,
, 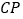 平分
平分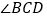 的外角
的外角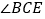 ,猜想
,猜想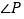 与
与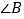 、
、 的数量关系是______;
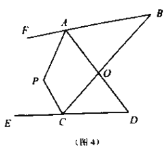
的数量关系是______;(2)如图(4),直线
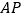 平分
平分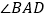 的外角
的外角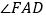 ,
, 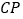 平分
平分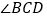 的外角
的外角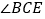 ,猜想
,猜想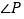 与
与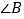 、
、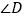 的数量关系,并说明理由.
的数量关系,并说明理由.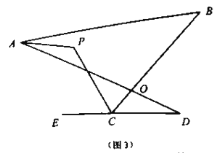
-
科目: 来源: 题型:
查看答案和解析>>【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=
 ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
A.1
B.2
C.3
D.4
相关试题

