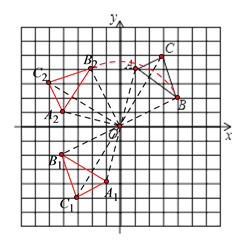
【题目】如图所示，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5）（每个方格的边长均为1个单位长度）

（1）请画出△A1B1C1，使△A1B1C1与△ABC关于原点对称；

（2）将△ABC绕点O逆时针旋转90°，画出旋转后得到的△A2B2C2，并直接写出线段OB旋转到OB2扫过图形的面积．

参考答案：

【答案】(1)见解析；（2）见解析，

【解析】试题分析：

（1）连接AO并延长至A1，使A1O=AO得到点A1，同法作出点B1、C1，顺次连接所得三点，即可得到所求三角形；

（2）过点O在AO的左侧作A2O⊥AO，使A2O=AO得到点A2，同法作出点B2、C2，顺次连接三点，即可得到所求三角形；由题意可知旋转过程中线段OB扫过的图形的面积就是扇形B2OB的面积，由题意可知∠B2OB=90°，再由勾股定理求出OB的长即可求得所求面积了.

试题解析：

（1）如下图，△即为所求三角形；（2）①如下图，△即为所求三角形；

②由题意可知：旋转过程中线段OB扫过的图形的面积就是扇形B2OB的面积，

∵∠B2OB=90°，OB=，

∴S扇形B2OB=.

∴旋转过程中线段OB扫过的图形的面积为： .

关闭