【题目】如图所示,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.

(1)求证:四边形EFDG是菱形;
(2)求证:EG2=![]() GF×AF;
GF×AF;
(3)若![]() ,折痕AF=5
,折痕AF=5![]() cm,则矩形ABCD的周长为 .
cm,则矩形ABCD的周长为 .
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)36cm.
【解析】试题分析:(1)先依据翻折的性质和平行线的性质证明∠DGF=∠DFG,从而得到GD=DF,接下来依据翻折的性质可证明DG=GE=DF=EF。
(2)连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF=![]() GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系.
GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系.
(3)过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FGH∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD-GH求解即可.
试题解析:
(1)证明:如图所示,
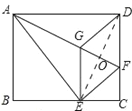
∵EG∥CD, ∴∠EGF=∠DFG.
∵由折叠的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG. ∴GD=DF.
∴GD=GE=DF=EF,∴四边形EFDG为菱形;
(2)证明:如图所示,连接DE,交AF于点O.
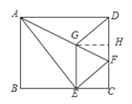
∵四边形EFDG为菱形, ∴GF⊥DE,OG=OF=![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA, ∴△DOF∽△ADF.
∴![]() ,即DF2=OFAF.
,即DF2=OFAF.
∵OF=![]() GF,DF=EG, ∴EG2=
GF,DF=EG, ∴EG2=![]() GFAF ;
GFAF ;
(3)矩形ABCD的周长为36 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=3,AB=5,D为AB边上一点,DE∥AC,交BC于点E,DF∥BC,交AC于点F,连接EF,则线段EF的最小值为

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校9名同学的身高(单位:cm)分别是:163,165,167,164,165,166,165,164,166,则这组数据的众数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD=
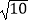 ,CD=2,BC=4,则AC=
,CD=2,BC=4,则AC= 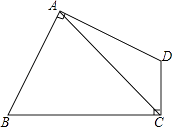
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察图,解答下列问题.
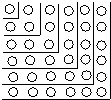
(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,…,第六层有11个圆圈.如果要你继续画下去,那么第八层有几个小圆圈?第n层呢?
(2)某一层上有65个圆圈,这是第几层?
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22 ,
由此得,1+3=22 .
同样,
由前三层的圆圈个数和得:1+3+5=32 .
由前四层的圆圈个数和得:1+3+5+7=42 .
由前五层的圆圈个数和得:1+3+5+7+9=52 .
…
根据上述请你猜测,从1开始的n个连续奇数之和是多少?用公式把它表示出来.
(4)计算:1+3+5+…+99的和;
(5)计算:101+103+105+…+199的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】包括中国志愿者王跃在内的6名志愿者踏上了为期12480小时的“火星之旅”.将12480用科学记数法表示应为( )
A. 12.48×103 B. 0.1248×105 C. 1.248×104 D. 1.248×103
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(2,﹣3)在反比例函数y=
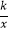 的图像上.
的图像上.
(1)试判断点B(﹣1,6),C(﹣3,﹣2)是否在这个反比例函数的图像上,请说明理由;
(2)若P(a﹣1,b),Q(a,c)也在这个反比例函数的图像上,且a<0,试比较b,c的大小.
相关试题

