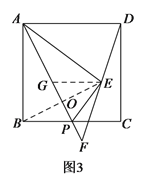
【题目】如图,边长为2的正方形ABCD,点P在射线BC上,将△ABP沿AP向右翻折,得到△AEP,DE所在直线与AP所在直线交于点F.
(1)如图1,当点P在边BC上时:
①若∠BAP=30°,求∠AFD的度数;
②若点P是BC边上任意一点时(不与B,C重合),∠AFD的度数是否会发生变化?试证明你的结论;
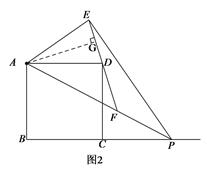
(2)如图2,若点P在BC边的延长线上时,∠AFD的度数是否会发生变化?试在图中画出图形,并直接写出结论;
(3)是否存在这样的情况,点E为线段DF的中点,如果存在,求BP的值;如果不存在,请说明理由.

参考答案:
【答案】(1)①∠AFD的度数为45°;②∠AFD的度数不会发生变化,证明见解析;
(2)画出图形见解析,∠AFE 的大小不会改变,理由见解析;
(3)BP的值为1.
【解析】(1)①∵∠EAP =∠BAP =30°,∴∠DAE =90°-30°×2=30°.
∵在△ADE中,AD =AE,∠DAE =30°,
∴∠ADE =∠AED =(180°﹣30°)÷2=75°.
∵在△AFD中,∠FAD =30°﹢30°=60°,∠ADF =75°,
∴∠F =180°﹣60°﹣75°=45°.
②方法一:
作AG⊥DF于G ,
∵在△ADE在,AD =AE,AG ⊥DE ,
∴AG平分∠DAE,∠2=∠DAG.
∵∠1=∠BAP,
∴∠1﹢∠2 =![]() ×90°=45°.
×90°=45°.
∴∠F =90°﹣45°=45°.
方法二:
②设∠BAP =∠EAP = ![]() ,则∠EAD=90°-2
,则∠EAD=90°-2![]() ,∠FAD=90°-
,∠FAD=90°- ![]() .
.
∵在△ADE中,AD =AE,∠EAD=90°-2![]() ,
,
∴∠ADE=![]() (180°-∠EAD)=
(180°-∠EAD)= ![]() (180°-90°+2
(180°-90°+2![]() )=45°+
)=45°+ ![]() .
.
∴在△ADF中,∠F=180°-∠FAD-∠ADE=180°-(90°- ![]() )-(45°+
)-(45°+ ![]() )=45°.
)=45°.
(2)方法一:
作图如图2所示,∠AFE 的大小不会改变.作AG⊥DE于G ,得∠DAG =∠EAG ,
设∠DAG =∠EAG = ![]() .
.
∴∠BAE =90°+2![]() .
.
∴∠FAE =![]() ∠BAE =45°+
∠BAE =45°+ ![]() .
.
∴∠FAG =∠FAE -∠EAG =45°.
方法二:
(2) ∠AFD 的大小不会改变.
设∠BAP =∠EAP = ![]() ,则∠EAD=2
,则∠EAD=2![]() -90° ,
-90° ,
∵在△ADE中,AD =AE,∠EAD=2![]() -90°,
-90°,
∴∠AED=![]() (180°-∠EAD)=
(180°-∠EAD)= ![]() (180°-2
(180°-2![]() +90°)=135°-
+90°)=135°- ![]() .
.
∴在△AEF中, ∠AFD=180°-∠FAE-∠AED=180°- ![]() -(135°-
-(135°- ![]() )=45°.
)=45°.
(3)存在点E为DF的中点.
连接BE交AF于点O,作EG∥AD,得EG∥BC.
∵EG∥AD,DE=EF,
∴EG=![]() AD=1.
AD=1.
∵AB=AE,∴点A在线段BE的垂直平分线上.
同理得:点P在线段BE的垂直平分线上.
∴AF垂直平分线段BE.
∴OB=OE.
∵GE∥BP,∴∠OBP=∠OEG,∠OPB=∠OGE.
∴BP=EG=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蛋糕生产厂家想就产品的价格以及质量进行一项简单的调查,调查问题为:你认为我厂生产的蛋糕是否品质纯正而且价格优惠?A.是;B.否.你觉得调查问题的设计有什么值得改进的地方吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形的两条对角线长和一条边的长可以依次是( )
A.4、4、4
B.6、4、4
C.6、4、6
D.3、4、5 -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的多项式(x-m)与(x+7)的积的常数项为14,则m的值是()
A. 2 B. -2 C. 7 D. -7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=﹣1.
(1)求抛物线对应的函数关系式;
(2)点P在y轴上,点M在x轴正方向上,过点M作x轴的垂线交抛物线于点C,OP=3OM.
①当四边形OMCP为矩形时,求OM的长;
②过点C作x轴的平行线,交抛物线于另一点D,求点P在直线CD的下方时,求CD的取值范围.

-
科目: 来源: 题型:
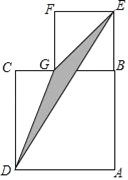
查看答案和解析>>【题目】如图,正方形ABCD与正方形BEFG,且A,B,E在一直线上,已知AB=a,BE=b(b<a).
(1)用a、b的代数式表示△ADE的面积.
(2)用a、b的代数式表示△DCG的面积.
(3)用a、b的代数式表示阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】AD是△ABC的边BC上的中线,AB=6,AC=4,则边BC的取值范围是 , 中线AD的取值范围是 .
相关试题

