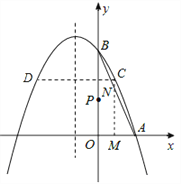
【题目】如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=﹣1.
(1)求抛物线对应的函数关系式;
(2)点P在y轴上,点M在x轴正方向上,过点M作x轴的垂线交抛物线于点C,OP=3OM.
①当四边形OMCP为矩形时,求OM的长;
②过点C作x轴的平行线,交抛物线于另一点D,求点P在直线CD的下方时,求CD的取值范围.

参考答案:
【答案】(1)抛物线的解析式为:y=-(x+1)2+4或![]() ;
;
(2)①当OM=![]() 时,四边形OMCP为矩形;
时,四边形OMCP为矩形;
②点P在直线CD的下方时,CD的取值范围是2<CD<![]() .
.
【解析】解:(1)根据题意,设抛物线的解析式为:y=a(x+1)2+k,
∵点A(1,0),B(0,3)在抛物线上,
∴![]() ,
,
解得:a=﹣1,k=4,
∴抛物线的解析式为:y=-(x+1)2+4或![]() .
.
(2)①∵当四边形OMCP为矩形时,设OM= t,则OP=3 t,
则有OP=MC,即3t=-(t+1)2+4,
整理得:t2+5t﹣3=0,
解得t=![]() ,由于t=
,由于t=![]() <0,故舍去,
<0,故舍去,
∴当OM=![]() 时,四边形OMCP为矩形;
时,四边形OMCP为矩形;
②∵设OM= t时,函数y=-(t+1)2+4的对称轴为![]() ,
,
∴点C到直线![]() 的距离为t+1.
的距离为t+1.
∴CD=2 t+2.
 ∵当OM=
∵当OM=![]() 时,四边形OMCP为矩形,
时,四边形OMCP为矩形,
此时OP=![]() ,点P在CD上,
,点P在CD上,
∴点P在直线CD的下方时,t =OM<![]() .
.
∵CD=2 t+2,
∴CD<![]()
又∵点C与点B重合时, CD=2,点M在x轴正方向上,
∴求点P在直线CD的下方时,CD的取值范围是2<CD<![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形的两条对角线长和一条边的长可以依次是( )
A.4、4、4
B.6、4、4
C.6、4、6
D.3、4、5 -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的多项式(x-m)与(x+7)的积的常数项为14,则m的值是()
A. 2 B. -2 C. 7 D. -7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的正方形ABCD,点P在射线BC上,将△ABP沿AP向右翻折,得到△AEP,DE所在直线与AP所在直线交于点F.
(1)如图1,当点P在边BC上时:
①若∠BAP=30°,求∠AFD的度数;
②若点P是BC边上任意一点时(不与B,C重合),∠AFD的度数是否会发生变化?试证明你的结论;
(2)如图2,若点P在BC边的延长线上时,∠AFD的度数是否会发生变化?试在图中画出图形,并直接写出结论;
(3)是否存在这样的情况,点E为线段DF的中点,如果存在,求BP的值;如果不存在,请说明理由.

-
科目: 来源: 题型:
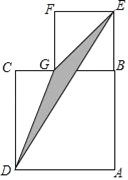
查看答案和解析>>【题目】如图,正方形ABCD与正方形BEFG,且A,B,E在一直线上,已知AB=a,BE=b(b<a).
(1)用a、b的代数式表示△ADE的面积.
(2)用a、b的代数式表示△DCG的面积.
(3)用a、b的代数式表示阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】AD是△ABC的边BC上的中线,AB=6,AC=4,则边BC的取值范围是 , 中线AD的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:将代数式x2+2x+3转化为(x+m)2+k的形式(其中m,k为常数),则x2+2x+3=x2+2x+1﹣1+3=(x+1)2+2,其中m=1,k=2.
(1)仿照此法将代数式x2+6x+15化为(x+m)2+k的形式,并指出m,k的值.
(2)若代数式x2﹣6x+a可化为(x﹣b)2﹣1的形式,求b﹣a的值.
相关试题

