【题目】如图,矩形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
(1)求AE的长;
(2)当t为何值时,△PAE为直角三角形?

参考答案:
【答案】(1)5;(2)当t=6或t=![]() 时,△PAE为直角三角形;
时,△PAE为直角三角形;
【解析】
(1)在直角△ADE中,利用勾股定理进行解答;
(2)需要分类讨论:AE为斜边和AP为斜边两种情况下的直角三角形;
解:(1)∵矩形ABCD中,AB=9,AD=4,
∴CD=AB=9,∠D=90°,
∴DE=9﹣6=3,
∴AE=![]() =5;
=5;
(2)①若∠EPA=90°,t=6;
②若∠PEA=90°,(6﹣t)2+42+52=(9﹣t)2,
解得t=![]() .
.
综上所述,当t=6或t=![]() 时,△PAE为直角三角形;
时,△PAE为直角三角形;
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两站相距480千米,一辆快车从甲站出发,每小时行驶120千米,一辆慢车从乙站出发,每小时行驶80千米.
(1)两车同时开出,相向而行,多少小时后两车相遇?
(2)两车同时开出,相向而行,多少小时后两车相距100千米?
-
科目: 来源: 题型:
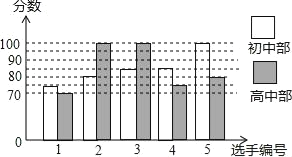
查看答案和解析>>【题目】某学校举行“中国梦,我的梦”演讲比赛,初、高中部根据初赛成绩,各选出5名选手组成代表队决赛,初、高中部代表队的选手决赛成绩如图所示:
(1)根据图示填写表格:
平均数(分)
中位数(分)
众数(分)
初中代表队
85
85
高中代表队
80
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明上周零花钱使用情况:(规定:超过50元记为正,少于50元记为负)
星期一
星期二
星期三
星期四
星期五
+11
+10
﹣17
+18
﹣12
请你解答以下问题:
(1)上星期五小明用了多少零花钱;
(2)上星期四比上星期三多花了多少零花钱;
(3)求上周平均每天用多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2,交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积.

-
科目: 来源: 题型:
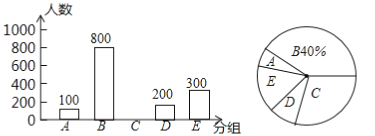
查看答案和解析>>【题目】为调查市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:
(1)在这次调查中,一共调查了 名市民.
(2)扇形统计图中,C组对应的扇形圆心角是 .
(3)请补全条形统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点A,B分别对应数a,b.其中a<0,b>0.
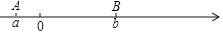
(1)当a=﹣2,b=6时,求a-b=_____,线段AB的中点对应的数是 ;(直接填结果)
(2)若该数轴上另有一点M对应着数m.
①当a=﹣4,b=8,点M在A,B之间,且AM=3BM时,求m的值.
②当m=2,b>2,且AM=2BM时,求代数式a+2b+20的值.
相关试题

