【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 .
(1)EF=![]() OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=![]() OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(5)OGBD=AE2+CF2.
;(5)OGBD=AE2+CF2.

参考答案:
【答案】(1),(2),(3),(5).
【解析】
试题分析:(1)∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,
∴∠BOF+∠COF=90°,
∵∠EOF=90°,
∴∠BOF+∠COE=90°,
∴∠BOE=∠COF,
在△BOE和△COF中,
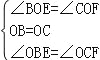 ,
,
∴△BOE≌△COF(ASA),
∴OE=OF,BE=CF,
∴EF=![]() OE;故正确;
OE;故正确;
(2)∵S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC=![]() S正方形ABCD,
S正方形ABCD,
∴S四边形OEBF:S正方形ABCD=1:4;故正确;
(3)∴BE+BF=BF+CF=BC=![]() OA;故正确;
OA;故正确;
(4)过点O作OH⊥BC,
∵BC=1,
∴OH=![]() BC=
BC=![]() ,
,
设AE=x,则BE=CF=1﹣x,BF=x,
∴S△BEF+S△COF=![]() BEBF+
BEBF+![]() CFOH=
CFOH=![]() x(1﹣x)+
x(1﹣x)+![]() (1﹣x)×
(1﹣x)×![]() =﹣
=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∵a=﹣![]() <0,
<0,
∴当x=![]() 时,S△BEF+S△COF最大;
时,S△BEF+S△COF最大;
即在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;故错误;
;故错误;
(5)∵∠EOG=∠BOE,∠OEG=∠OBE=45°,
∴△OEG∽△OBE,
∴OE:OB=OG:OE,
∴OGOB=OE2,
∵OB=![]() BD,OE=
BD,OE=![]() EF,
EF,
∴OGBD=EF2,
∵在△BEF中,EF2=BE2+BF2,
∴EF2=AE2+CF2,
∴OGBD=AE2+CF2.故正确.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a=5,2b=1,求2a+b+3的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的三个顶点的坐标分别是A(1,2),B(-1,-2),C(-2,3),将其平移到点A/处,使A与A/(-1,-3)重合,则B、C两点平移后的坐标分别是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若CD=15,BE=10,tanA=
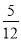 ,求⊙O的直径.
,求⊙O的直径.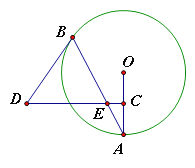
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条开口向下的抛物线的顶点坐标是(2,3),则这条抛物线对应的函数有( )
A. 最大值3 B. 最小值3 C. 最大值2 D. 最小值-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F、G、H分别为菱形ABCD四边的中点,AB=6cm,∠ABC=60°,则四边形EFGH的面积为__cm2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知xm=6,xn=3,则x2m﹣n的值为( )
A.9
B.39
C.12
D.108
相关试题

