Question

【题目】如图，等腰三角形ABC中，AC=BC=10，AB=12．

（1）动手操作：利用尺规作以BC为直径的⊙O，⊙O交AB于点D，⊙O交AC于点E，并且过点D作DF⊥AC交AC于点F．

（2）求证：直线DF是⊙O的切线；

（3）连接DE，记△ADE的面积为S1，四边形DECB的面积为S2，求的值．

Answer 1

【答案】（1）作图见解析；（2）证明见解析；（3）=．

【解析】试题分析：（1）根据题意作出图形即可；

（2）连接OD，根据等腰三角形的性质得到∠A=∠ODB根据平行线的判定得到OD∥AC，由平行线的性质得到∠ODF=∠AFD=90°，于是得到结论；

（3）连接DE；根据圆周角定理得到∠CDB=90°，即CD⊥AB，由等腰三角形的性质得到AD=BD=AB=6，根据圆内接四边形的性质得到∠BDE+∠C=180°，等量代换得到∠C=∠ADE，根据相似三角形的性质得到，于是得到结论．

试题解析：（1）如图所示，图形为所求；

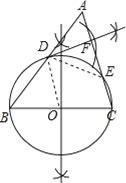
（2）连接OD

∵DF⊥AC，∴∠AFD=90°，

∵AC=BC∴∠A=∠B，

∵OB=OD，∴∠B=∠ODB，∴∠A=∠ODB∴OD∥AC，

∴∠ODF=∠AFD=90°，∴直线DF是⊙O的切线；

（3）连接DE；

∵BC是⊙O的直径，∴∠CDB=90°，即CD⊥AB，

∵AC=BC，CD⊥AB，∴AD=BD=AB=6，

∵四边形DECB是圆内接四边形，∴∠BDE+∠C=180°，

∵∠BDE+∠ADE=180°，∴∠C=∠ADE，

∵在△ADE和△ACB中，∠ADE=∠C，∠DAE=∠CAB，

∴△ADE∽△ACB，∴，∴，

∵S△ABC=S△ADE+S四边形DECB，∴ ，

∴，即=．