【题目】如图,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 移动,同时,点
移动,同时,点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 的延长线移动,已知点
的延长线移动,已知点![]() 、
、![]() 的移动速度相同,
的移动速度相同,![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
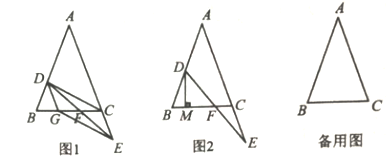
(1)如图1,当点![]() 在线段
在线段![]() 上时,过点
上时,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,求证:点
,求证:点![]() 是
是![]() 的中点;
的中点;
(2)如图2,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,当点
,当点![]() 、
、![]() 在移动过程中,线段
在移动过程中,线段![]() 、
、![]() 、
、![]() 有何数量关系?请直接写出你的结论: .
有何数量关系?请直接写出你的结论: .
参考答案:
【答案】(1)见解析;(2)![]() 或
或![]() .
.
【解析】
(1)由题意得出BD=CE,由平行线的性质得出∠DGB=∠ACB,由等腰三角形的性质得出∠B=∠ACB,得出∠B=∠DGB,证出BD=GD=CE,即可得出结论;
(2)由(1)得:BD=GD=CE,由等腰三角形的三线合一性质得出BM=GM,由平行线得出GF=CF,即可得出结论.
(1)四边形CDGE是平行四边形.理由如下:
∵D、E移动的速度相同,
∴BD=CE,
∵DG∥AE,
∴∠DGB=∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠DGB,
∴BD=GD=CE,
又∵DG∥CE,
∴四边形CDGE是平行四边形;
(2)当点D在AB边上时,BM+CF=MF;理由如下:
如图2,
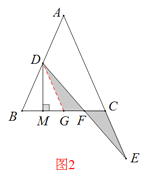
由(1)得:BD=GD=CE,
∵DM⊥BC,
∴BM=GM,
∵DG∥AE,
∴GF=CF,
∴BM+CF=GM+GF=MF.
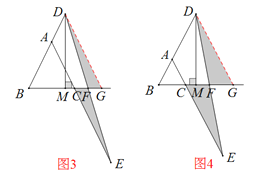
同理可证,当D点在BA的延长线上时,可证![]() , 如图3,4.
, 如图3,4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个整数能表示成a2+b2(a、b是正整数)的形式,则称这个数为“完美数”。例如5是“完美数”,因为5=22+12,再如M=x2+2xy+2y2=(x+y)2 +y2(x、y是正整数),所以M也是“完美数”。
(1)请你再写一个小于10的“完美数”,并判断29是否为“完美数”;
(2)试判断(x2+9y2)(4y2+x2)(x、y是正整数)是否为“完美数”,并说明理由;
(3)已知S=x2+4y2+4x-12y+k(x、y是正整数,k是常数),要使S为“完美数”,试求出符合条件的一个k值,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解是数学解题的一种重要工具,掌握不同因式分解的方法对数学解题有着重要的意义.我们常见的因式分解方法有:提公因式法、公式法、分组分解法、十字相乘法等.在此,介绍一种方法叫“试根法”.例:
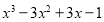 ,当
,当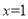 时,整式的值为0,所以,多项式有因式
时,整式的值为0,所以,多项式有因式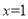 ,设
,设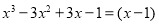
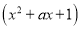 ,展开后可得
,展开后可得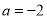 ,所以
,所以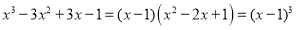 ,根据上述引例,请你分解因式:
,根据上述引例,请你分解因式:(1)
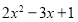 ;
;(2)
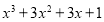 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC为直径作
 交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.(1)求证: EF与
 相切;
相切;(2)若AE=6,
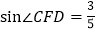 ,求EB的长.
,求EB的长.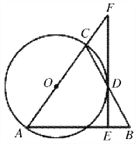
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
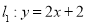 与
与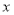 轴交于点
轴交于点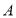 ,与
,与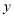 轴交于点
轴交于点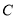 ;直线
;直线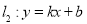 与
与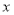 轴交于点
轴交于点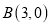 ,与直线
,与直线 交于点
交于点 ,且点
,且点 的纵坐标为4.
的纵坐标为4.
(1)不等式
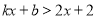 的解集是 ;
的解集是 ;(2)求直线
 的解析式及
的解析式及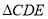 的面积;
的面积;(3)点
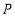 在坐标平面内,若以
在坐标平面内,若以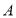 、
、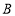 、
、 、
、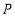 为顶点的四边形是平行四边形,求符合条件的所有点
为顶点的四边形是平行四边形,求符合条件的所有点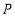 的坐标.
的坐标. -
科目: 来源: 题型:
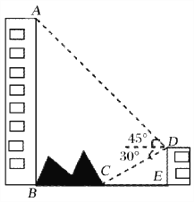
查看答案和解析>>【题目】如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上). 已知AB=80m,DE=10m,求障碍物B,C两点间的距离.(结果精确到0.1m)
(参考数据:
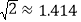 ,
,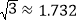 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>6且x<14,单位km)

(1)这辆出租车第三次行驶完后在离出发点的 方向;经过连续4次行驶后,这辆车所在的位置 (结果用表示);
(2)这辆出租车一共行驶了多少路程(结果用表示);当x=8时,出租车行驶的路程是多少 .
相关试题

